korrelációs együttható
mennyire jól képviseli a regressziós egyenlet valóban
az adatkészletet?
a kérdésre adott válasz meghatározásának egyik módja a korrelációs együttható és a meghatározási együttható vizsgálata.,
|
|
a korrelációs együttható, r, és |
amellett, hogy megjelenik a regressziós információ, az értékek rand r 2 megtalálható underVARS, #5 statisztika → EQ #7 r és #8 r 2 .,
korrelációs együttható, r:
az R mennyiség, amelyet lineáris korrelációs együtthatónak neveznek, megméri a két változó közötti lineáris kapcsolat erősségét és
irányát. A lineáris korreláció
együtthatót néha Pearson termék pillanatnyi korrelációs együtthatójának nevezik a fejlesztő Karl Pearson tiszteletére.
a computingr matematikai képlete: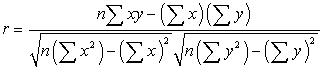
ahol n az adatpárok száma.,
(nem örülsz, hogy van egy grafikus számológép, amely kiszámítja ezt a képletet?) az R értéke olyan, hogy -1< r < +1. A + és-jeleket pozitív
lineáris korrelációkra, illetve negatív lineáris korrelációkra használjuk.
pozitív korreláció: ha x és y erős pozitív lineáris korrelációval rendelkezik,r közel van
a +1-hez. A pontosan + 1 r érték tökéletes pozitív illeszkedést jelez., A pozitív értékek
jelzik az x és y változók közötti kapcsolatot, például az X értékei nőnek, az y értékei is növekednek.
negatív korreláció: ha x és y erős negatív lineáris korrelációval rendelkezik,r közel van
-1-hez. A pontosan -1 r érték tökéletes negatív illeszkedést jelez. A negatív értékek
jelzik az x és y közötti kapcsolatot, úgy, hogy az X értékek növekednek,az értékek
az y csökkenés. nincs korreláció: ha nincs lineáris korreláció vagy gyenge lineáris korreláció, r
közel 0., A nulla közeli érték azt jelenti, hogy a
két változó között véletlenszerű, nemlineáris kapcsolat van vegye figyelembe, hogy r dimenzió nélküli mennyiség; vagyis nem függ a
alkalmazott egységektől.
a ± 1 tökéletes korreláció csak akkor fordul elő, ha az adatpontok pontosan egy
egyenes vonalban fekszenek. Ha r = + 1, ennek a vonalnak a lejtése pozitív. Ha r = -1, ennek a
vonalnak a lejtése negatív. a 0,8-nál nagyobb korrelációt általában erősnek, míg a korrelációt
0-nál kisebbnek írják le.,Az 5-öt általában úgy írják le, mintgyenge. Ezek az értékek a vizsgált adatok
“típusa” alapján változhatnak. A tudományos adatokat használó tanulmány erősebb
korrelációt igényelhet, mint a társadalomtudományi adatokat használó tanulmány.
determinációs Együttható, r 2, vagy R2 :
A determinációs együttható, r 2,hasznos, mert ez ad aránya
a variancia (fluktuáció) egy változó, hogy kiszámítható a többi változó.,
Ez egy olyan intézkedés, amely lehetővé teszi számunkra, hogy meghatározzuk, mennyire lehet bizonyos a
előrejelzések készítése egy bizonyos modellből/grafikonból.
a meghatározási együttható a magyarázott variáció aránya a teljes
variációhoz. a meghatározási együttható olyan, hogy 0 < r 2 < 1, és az x és y közötti lineáris asszociáció
erősségét jelöli.,
a meghatározási együttható az adatok százaléka, amely a legközelebb áll a legjobb illeszkedéshez. Például, ha r = 0,922, akkor r 2 = 0,850, ami azt jelenti, hogy
az iny teljes variációjának 85% – a magyarázható az x
és y közötti lineáris összefüggéssel(a regressziós egyenlet szerint). A többi 15% a teljes variáció
y továbbra is megmagyarázhatatlan. a meghatározási együttható annak mértéke, hogy a
regressziós vonal mennyire képviseli az adatokat., Ha a regressziós vonal pontosan áthalad a
scatter telek minden pontján, akkor képes lenne megmagyarázni az összes variációt. Minél tovább a vonal
távol a pontoktól, annál kevésbé képes megmagyarázni.