
Ebben a cikkben megtudhatja, SVM vagy Support Vector Machine, ami az egyik legnépszerűbb AI algoritmusok (ez az egyik top 10-AI algoritmusok), valamint arról, hogy a Kernel Trükk, amely foglalkozik a nem-linearitás, valamint a magasabb dimenziók., Megérintjük témák, mint a hyperplanes, Lagrange szorzók, mi lesz vizuális példák és kód példák (hasonló a kód példa használt KNN fejezet), hogy jobban megértsük ezt a nagyon fontos algoritmus.
SVM Explained
A Support Vector Machine egy felügyelt tanulási algoritmus, amelyet többnyire osztályozáshoz használnak, de regresszióhoz is használható. A fő ötlet az, hogy a jelzett adatok (képzési adatok) alapján az algoritmus megpróbálja megtalálni az optimális hiperplántot, amely új adatpontok osztályozására használható. Két dimenzióban a hyperplane egy egyszerű vonal.,
általában egy tanulási algoritmus megpróbálja megtanulni egy osztály leggyakoribb jellemzőit (ami megkülönbözteti az egyik osztályt a másiktól), a besorolás pedig a tanult reprezentatív jellemzőkön alapul (tehát az osztályozás az osztályok közötti különbségeken alapul). Az SVM fordítva működik. Megtalálja a leginkább hasonló példákat az osztályok között. Ezek lesznek a támogató Vektorok.
mint például, lehetővé teszi, hogy fontolja meg a két osztály, alma, citrom.,
más algoritmusok megtanulják az alma és a citrom legnyilvánvalóbb, legjellemzőbb tulajdonságait, mint például az alma zöld és lekerekített, míg a citrom sárga és elliptikus.
ezzel szemben az SVM olyan almákat keres, amelyek nagyon hasonlítanak a citromra, például a sárga és elliptikus formájú almákra. Ez egy támogató vektor lesz. A másik támogató vektor egy Almához hasonló citrom (zöld és lekerekített) lesz. Tehát más algoritmusok megtanulják a különbségeket, miközben az SVM megtanulja a hasonlóságokat.,
Ha megjelenítjük a fenti példa 2D-ben, akkor lesz valami, mint ez:

Ahogy haladunk, balról jobbra, a példák kell besorolni, mint az alma, amíg el nem érjük a sárga alma. Ettől a ponttól kezdve az a bizalom, hogy egy új példa az alma, csökken, miközben a citrom osztály bizalma nő., Amikor a citrom osztály magabiztossága nagyobb lesz, mint az alma osztály bizalma, az új példákat citromnak kell besorolni (valahol a sárga alma és a zöld citrom között).
Ezen támogató Vektorok alapján az algoritmus megpróbálja megtalálni a legjobb hiperplántot, amely elválasztja az osztályokat. 2D-ben a hyperplane egy sort, így fog kinézni:

Ok, de miért rajzoltam a kék határa, mint a fenti képen?, Én is léptem át a határt, mint ez:

Mint látható, nálunk a lehetőségek száma végtelen felhívni a határozat határ. Szóval hogyan találjuk meg az optimálisat?
az optimális Hiperplán megtalálása
intuitív módon a legjobb vonal az a vonal, amely messze van mind az alma, mind a citrom példáitól (a legnagyobb margóval rendelkezik)., Az optimális megoldás érdekében mindkét módon maximalizálnunk kell a margót (ha több osztályunk van, akkor maximalizálnunk kell az egyes osztályok figyelembevételével).

Szóval, ha összehasonlítjuk a fenti képen, a kép alatt, könnyen megfigyelhetjük, hogy az első az optimális hyperplane (a vonal), a második pedig egy szub-optimális megoldás, mert a különbözet jóval rövidebb.,

Mert azt akarjuk, hogy maximalizálja a margók veszi figyelembe, csak az osztályok, ahelyett, hogy egy margó minden osztály, használjuk a “globális” margin, amely veszi figyelembe az összes osztályt., Ezt a különbözetet úgy nézne ki, mint a lila vonal a következő kép:

Ez a különbözet merőleges a határ pedig egyenlő távolságra, hogy a támogatás vektorok.
tehát hol vannak Vektorok? Minden számítást (távolság és optimális hiperplánok kiszámítása) vektoros térben végzünk, így minden adatpontot vektornak tekintünk. A tér dimenzióját a példák attribútumainak száma határozza meg., Ahhoz, hogy megértsük a matematikai mögött, kérjük, olvassa el ezt a rövid matematikai leírása Vektorok, hiperplánok és optimalizációk: SVM tömören.
összességében a support Vektorok olyan adatpontok, amelyek meghatározzák a hiperplán helyzetét és margóját. “Támogató” vektoroknak nevezzük őket, mivel ezek az osztályok reprezentatív adatpontjai, ha az egyiket mozgatjuk, a pozíció és/vagy a margó megváltozik. Más adatpontok mozgatása nem lesz hatással a margóra vagy a hiperplán helyzetére.,
az osztályozáshoz Nincs szükségünk az összes képzési adatpontra (mint például a KNN esetében), csak a támogató vektorokat kell mentenünk. A legrosszabb esetben az összes pont támogatja a vektorokat, de ez nagyon ritka, ha ez megtörténik, akkor ellenőrizze a modell hibáit vagy hibáit.
tehát alapvetően a tanulás egyenértékű a hyperplane megtalálásával a legjobb margóval, tehát ez egy egyszerű optimalizálási probléma.,/h2>
Az alapvető lépéseket az SVM a következők:
- válassza ki a két hyperplanes (2D), amely elválasztja az adatok nem pont között (piros vonalak)
- maximalizálják a távolság (a margó)
- az átlagos vonal (itt a vonal között félúton van a két piros vonal) majd a döntést határ
Ez nagyon szép lassan, de hogy a legjobb margó, a optimalizálási probléma nem triviális (könnyű 2D-ben, amikor már csak két attribútumok, de mi van, ha a N méretek N egy nagyon nagy szám)
megoldani az optimalizálási probléma, használjuk a Lagrange Multiplikátorok., Ahhoz, hogy megértsük ezt a technikát, akkor olvassa el a következő két cikket: kettősség Langrange szorzó és egy egyszerű magyarázat, hogy miért Langrange szorzók Wroks.
eddig lineárisan elválasztható adatok voltak, így egy sort osztályhatárként használhatunk. De mi van, ha nem lineáris adatkészletekkel kell foglalkoznunk?,
SVM a Nem-Lineáris adatsorok
Egy példa a nem-lineáris adatok:

Ebben az esetben nem tudunk találni egy egyenes vonal külön alma a citrom. Tehát hogyan tudjuk megoldani ezt a problémát. A Kernel trükköt fogjuk használni!
Az alapötlet az, hogy amikor egy adatkészlet elválaszthatatlan az aktuális dimenziókban, adjon hozzá egy másik dimenziót, talán így az adatok elválaszthatók lesznek., Gondolj csak bele, a fenti példa 2D-ben van, és elválaszthatatlan, de talán 3D-ben van különbség az alma és a citrom között, talán van egy szintkülönbség, tehát a citrom az első szinten van, a citrom pedig a második szinten van. Ebben az esetben az 1-es és a 2-es szint között könnyen rajzolhatunk egy elválasztó hiperplántot (3D-ben egy hiperplán egy sík).
magasabb dimenziók leképezése
a probléma megoldásához nem szabad csak vakon hozzáadni egy másik dimenziót, át kell alakítanunk a teret, hogy szándékosan generáljuk ezt a szintkülönbséget.,
leképezés 2D-ről 3D-re
feltételezzük, hogy hozzáadunk egy másik X3 nevű dimenziót. Egy másik fontos átalakulás az, hogy az új dimenzióban a pontokat az X12 + x22 képlet segítségével szervezik.
Ha az x2 + y2 képlet által meghatározott síkot ábrázoljuk, akkor valami ilyesmit kapunk:

/div>
most meg kell térképezni az alma és a citrom (amelyek csak egyszerű pontok), hogy ezt az új helyet. Gondold át alaposan, mit tettünk?, Csak egy átalakítást használtunk, amelyben a távolság alapján szinteket adtunk hozzá. Ha az eredetiben vagy, akkor a pontok a legalacsonyabb szinten lesznek. Ahogy távolodunk az eredettől, ez azt jelenti, hogy felmászunk a dombra (a sík közepétől a margók felé haladva), így a pontok szintje magasabb lesz., Most, ha figyelembe vesszük, hogy a származás, a citrom, a központ, akkor lesz valami, mint ez:
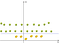
Most már könnyen szét a két osztály. Ezeket az átalakításokat magoknak nevezik. Népszerű kernelek: polinom Kernel, Gauss Kernel, radiális alapfunkció (RBF), Laplace RBF Kernel, Sigmoid Kernel, Anove RBF Kernel stb. (lásd Kernel funkciók vagy részletesebb leírás gépi tanulási kernelek).,
Leképezés 1D 2D
egy Másik, könnyebb például a 2D lenne:

Használata után a kernel után a transzformációk kapunk:

Tehát az átalakulás, könnyen behatárolják a két osztály segítségével csak egyetlen sort.,
a valós életben alkalmazott alkalmazásokban nem lesz egyszerű egyenes vonal, de sok görbével és nagy méretekkel rendelkezünk. Bizonyos esetekben nem lesz két hiperplánunk, amelyek pont nélkül elválasztják az adatokat, ezért szükségünk van néhány kompromisszum, tolerancia a kiugró értékekkel szemben. Szerencsére az SVM algoritmusnak van egy úgynevezett regularizációs paramétere a trade-off konfigurálásához és a kiugró értékek eltűréséhez.
Tuning paraméterek
ahogy az előző részben láttuk, a megfelelő kernel kiválasztása döntő fontosságú, mert ha az átalakulás helytelen, akkor a modell nagyon rossz eredményeket érhet el., Hüvelykujjszabályként mindig ellenőrizze, hogy van-e lineáris adat, ebben az esetben mindig használjon lineáris SVM-et (lineáris kernel). A lineáris SVM paraméteres modell, de az RBF kernel SVM nem, így az utóbbi összetettsége a képzési készlet méretével nő. Nem csak drágább, hogy a vonat egy RBF kernel SVM, de akkor is meg kell tartani a kernel mátrix körül, és a vetítés ebbe a “végtelen” magasabb dimenziós térben, ahol az adatok lineárisan elválasztható drágább, valamint a becslés során., Továbbá, több hiperparaméter van a beállításhoz, így a modellválasztás is drágább! Végül pedig sokkal könnyebb egy összetett modell túlterhelése!
Regularization
a Regularization paraméter (Pythonban C-nek hívják) megmondja az SVM optimalizálásnak, hogy mennyit szeretne elkerülni az egyes képzési példák osztályozásának elmulasztása.
Ha a C magasabb, akkor az optimalizálás kisebb margin hyperplane-t választ, így a képzési adatok miss osztályozási aránya alacsonyabb lesz.,
másrészt, ha a C alacsony, akkor a margó nagy lesz, még akkor is, ha hiányoznak a minősített képzési adatok példái. Ezt mutatja az alábbi két diagram:

Mint látható a képen, amikor a C alacsony, a különbözet magasabb (tehát implicit módon nincs olyan sok görbék, a vonal nem feltétlenül következik, az adatok pont) még akkor is, ha két almát sorolták, mint a citrom., Ha a C magas, a határ tele van görbékkel, és az összes képzési adatot helyesen osztályozták. Ne felejtsük el, hogy még akkor is, ha az összes képzési adatot helyesen osztályozták, ez nem jelenti azt, hogy a C növelése mindig növeli a pontosságot (a túlcsordulás miatt).
Gamma
a következő fontos paraméter a Gamma. A gamma paraméter meghatározza, hogy egy képzési példa milyen mértékben érinti el. Ez azt jelenti, hogy a magas Gamma csak a hihető hiperplánhoz közeli pontokat veszi figyelembe, az alacsony Gamma pedig nagyobb távolságú pontokat fog figyelembe venni.,

Mint látható, csökken a Gamma lesz az eredménye, hogy megtaláljuk a megfelelő hyperplane megfontolja, hogy pont a nagyobb távolságok, így egyre több pontot fog alkalmazni (zöld vonal jelzi, hogy melyik pontot tekintették, ha megtaláljuk az optimális hyperplane).
Margin
az utolsó paraméter a margó. Már beszéltünk margin, magasabb margin eredmények jobb modell, így jobb osztályozás (vagy becslés)., A margót mindig maximalizálni kell.
SVM példa Python
ebben a példában fogjuk használni a Social_Networks_Ads.csv fájl, ugyanaz a fájl, mint amit az előző cikkben használtunk, lásd a KNN példát a Python használatával.
ebben a példában csak az SVM és a KNN közötti különbségeket írom le, mert nem akarom megismételni magam minden cikkben! Ha azt szeretné, hogy a teljes magyarázatot, hogyan tudjuk elolvasni az adathalmazt, hogyan elemezzük és osztjuk meg adatainkat, vagy hogyan értékelhetjük vagy ábrázolhatjuk a döntés határait, akkor kérjük, olvassa el az előző fejezet (KNN) kódpéldáját!,
mivel a sklearn könyvtár egy nagyon jól megírt és hasznos Python könyvtár, nincs túl sok kódunk a módosításhoz. Az egyetlen különbség az, hogy meg kell importálni az SVC osztály (SVC = SVM sklearn) származó sklearn.svm helyett KNeighborsClassifier osztály sklearn.szomszédok.
az SVC importálása után létrehozhatjuk új modellünket az előre definiált konstruktor segítségével. Ennek a konstruktornak számos paramétere van, de csak a legfontosabbakat fogom leírni, legtöbbször nem használ más paramétereket.,
a legfontosabb paraméterek a következők:
- kernel: a használni kívánt kernel típus. A leggyakoribb kernelek az rbf (ez az alapértelmezett érték), a poly vagy a sigmoid, de saját kernelt is létrehozhat.,
- C: ez a regularization a paraméter leírása a Tuning Paraméterek szakasz
- gamma: ez is leírt a Tuning Paraméterek szakasz
- fok: ez csak akkor alkalmazzák, ha a választott kernel poli határozza meg a mértékét a polinom
- valószínűség: ez egy logikai paramétert, ha pedig ez igaz, akkor a modell visszatér minden jóslat, a vektor a valószínűsége tartozó minden osztály a válasz változó. Tehát alapvetően ez megadja a bizalmat az egyes előrejelzésekhez.,
- zsugorodás: ez azt mutatja, hogy szeretne-e zsugorodó heurisztikát használni az SVM optimalizálásában, amelyet szekvenciális minimális optimalizálásban használnak. Ez az alapértelmezett érték igaz, ha nincs jó oka, kérjük, ne változtassa meg ezt az értéket hamisra, mert a zsugorodás nagyban javítja a teljesítményt, a pontosság szempontjából a legtöbb esetben nagyon kevés veszteséggel.
most már láthatja a kód futtatásának kimenetét., A határozat határ a képzés meg így néz ki:

Mint láthatjuk, ahogy megtanultuk a Tuning Paraméterek szakasz mert a C-nek van egy kis érték (0.1) a határozat határ sima.
most, ha növeljük a C-t 0-ról.,1 100 további görbék a határozat határ:

Mi történne, ha a C=0.1 de most növeli a Gamma-a 0,1-10? Lássuk!

mi történt itt? Miért van ilyen rossz modellünk?, Amint azt a hangolási paraméterek szakaszban láttuk, a magas gamma azt jelenti, hogy a hihető hiperplán kiszámításakor csak olyan pontokat veszünk figyelembe, amelyek közel vannak. Mivel a zöld pontok sűrűsége csak a kiválasztott zöld régióban magas, ebben a régióban a pontok elég közel vannak a hihető hiperplánhoz, ezért ezeket a hiperplánokat választották. Legyen óvatos a gamma paraméterrel, mert ez nagyon rossz hatással lehet a modell eredményeire, ha nagyon magas értékre állítja (ami egy “nagyon magas érték”az adatpontok sűrűségétől függ).,
ebben a példában a C és a Gamma legjobb értékei 1,0 és 1,0. Most, ha elfogy a modell a vizsgált set mi lesz a következő ábra:

a Zűrzavar Mátrix így néz ki:

Mint látható, már csak 3 Téves Pozitív, de csak 4 Hamis Negatív., Ennek a modellnek a pontossága 93% , ami nagyon jó eredmény, jobb pontszámot kaptunk, mint a KNN használata (amelynek pontossága 80% volt).
megjegyzés: a pontosság nem az egyetlen metrikus, amelyet ML-ben használnak, és nem is a legjobb metrikus a modell értékeléséhez, a pontossági paradoxon miatt. Ezt a mutatót az egyszerűség kedvéért használjuk, de később a fejezet metrikák az AI algoritmusok értékeléséhez a pontossági paradoxonról fogunk beszélni, valamint bemutatom az ezen a területen használt más nagyon népszerű mutatókat.,
következtetések
ebben a cikkben láttunk egy nagyon népszerű és hatékony felügyelt tanulási algoritmust, a Support Vector Machine-t. Megtanultuk az alapötletet, hogy mi a hiperplán, mik a támogató vektorok és miért olyan fontosak. Sok vizuális ábrázolást is láttunk, amelyek segítettek abban, hogy jobban megértsük az összes fogalmat.
egy másik fontos téma, amelyet megérintettünk, a Kernel trükk, amely segített megoldani a nemlineáris problémákat.
ahhoz, hogy jobb modellünk legyen, láttuk az algoritmus hangolására szolgáló technikákat., A cikk végén volt egy Kódpéldánk a Python-ban, amely megmutatta nekünk, hogyan használhatjuk a KNN algoritmust.
végső gondolatként szeretnék néhány profit adni & hátrányok és néhány népszerű használati eset.,
Profik
- SVN lehet nagyon hatékony, mert csak az használ egy részét a képzési adatok, csak a támogatás vektorok
- nagyon jól Működik, a kisebb adathalmaz, a nem-lineáris adatállományok, valamint a magas dimenziós terek
- nagyon hatékony olyan esetekben, amikor a dimenziók száma nagyobb, mint a minták száma
- lehet nagy pontosságú, néha végre is jobb, mint a neurális hálózatok
- Nem nagyon érzékeny overfitting
Cons
- Képzési idő magas, amikor a nagy adathalmazok
- Ha az adatkészlet több zaj (én.,e. cél osztályok egymást átfedő) SVM nem jól teljesítenek
Népszerű használati Esetek
- Szöveg Besorolás
- Kimutatására spam
- Sentiment elemzés
- Szempont-alapú felismerés
- Szempont-alapú felismerés
- Kézzel írott jegyű elismerés
