hogyan működik a származékos számológép
azok számára, akiknek technikai háttere van, a következő szakasz ismerteti a származékos számológép működését.
először egy elemző elemzi a matematikai függvényt. Átalakítja egy olyan formává, amely jobban érthető egy számítógép, nevezetesen egy fa (lásd az alábbi ábrát). Ennek során a származékos számológépnek tiszteletben kell tartania a műveletek sorrendjét., A matematikai kifejezések különlegessége, hogy a szorzási jel néha kihagyható, például “5x” – et írunk az “5*x”helyett. A derivatív Kalkulátornak ezeket az eseteket kell felderítenie, és be kell illesztenie a szorzótáblát.
Az elemző JavaScript-ben kerül implementálásra, a tolatás-yard algoritmus alapján, közvetlenül a böngészőben futtatható. Ez lehetővé teszi a gyors visszajelzést gépelés közben átalakítja a fa LaTeX kódot. A MathJax gondoskodik arról, hogy megjelenítse a böngészőben.
amikor a “Go!,”gomb megnyomása után a derivatív kalkulátor elküldi a matematikai függvényt és a beállításokat (differenciálási változó és sorrend) a szervernek, ahol újra elemzik. Ezúttal a függvény átalakul egy olyan formává, amelyet a Maxima számítógépes algebra rendszer megérthet.
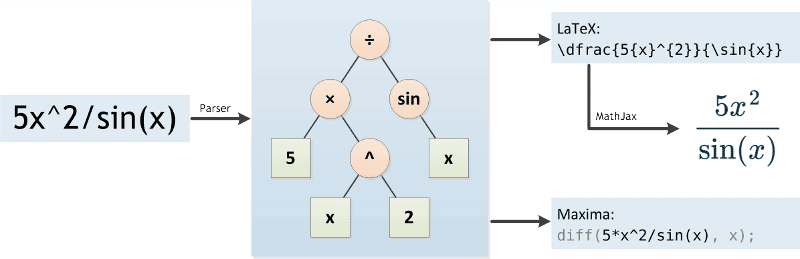
Maxima gondoskodik a matematikai függvény deriváltjának tényleges kiszámításáról. Mint minden számítógépes algebra rendszer, számos szabályt alkalmaz a függvény egyszerűsítésére és a származékok kiszámítására a közismert differenciálási szabályok szerint., A Maxima kimenete újra Latexné alakul, majd a felhasználó elé kerül.
a számítási lépések megjelenítése egy kicsit nagyobb szerepet játszik, mivel a származékos számológép nem függhet teljes mértékben a Maximától ehhez a feladathoz. Ehelyett a származékokat manuálisan kell kiszámítani lépésről lépésre. A differenciálás szabályait (termék szabály, hányados szabály, lánc szabály, …) JavaScript kódban hajtották végre. A trigonometrikus függvények és a négyzetgyök, logaritmusok és exponenciális függvények származékos függvényeinek táblázata is található., Minden számítási lépésben egy differenciálási műveletet hajtanak végre vagy átírnak. Például állandó tényezőket húznak ki a differenciálási műveletekből, az összegeket pedig felosztják (összegszabály). Ezt, valamint az Általános egyszerűsítéseket a Maxima végzi. Minden számított származék esetében a kapott matematikai kifejezések LaTeX ábrázolása a HTML-kódban van címkézve, így a kiemelés lehetséges.
A “válasz ellenőrzése” funkciónak meg kell oldania azt a nehéz feladatot, hogy meghatározza, hogy két matematikai kifejezés egyenértékű-e., Különbségüket a Maxima segítségével a lehető legnagyobb mértékben kiszámítják és egyszerűsítik. Például ez magában foglalja a trigonometrikus/hiperbolikus függvények írását exponenciális formáikban. Ha kimutatható, hogy a különbség nullára egyszerűsödik, a feladat megoldódik. Ellenkező esetben valószínűségi algoritmust alkalmaznak, amely mindkét funkciót véletlenszerűen kiválasztott helyeken értékeli és összehasonlítja.
az interaktív funkciógráfok a böngészőben kerülnek kiszámításra, és egy vászonelemen (HTML5) jelennek meg., Minden egyes grafikus funkcióhoz a számológép létrehoz egy JavaScript funkciót, amelyet kis lépésekben értékelnek a grafikon rajzolásához. A grafizálás során a szingularitásokat (pl. pólusokat) speciálisan detektálják és kezelik. A gesztusvezérlés kalapáccsal történik.js.
Ha bármilyen kérdése vagy ötlete van a származékos számológép fejlesztéséhez, ne habozzon, írjon nekem egy e-mailt.
