Schnelle Antwort:
Für ein rechtwinkliges Dreieck:

Die Sinusfunktion sin nimmt den Winkel θ und gibt das Verhältnis entgegengesetzte Hypotenuse
Die inverse Sinusfunktion sin-1 nimmt das Verhältnis entgegengesetztehypotenuse und gibt Winkel θ
Und Kosinus und Tangente folgen einer ähnlichen Idee.,
Und nun zu den Details:
Sinus, Kosinus und Tangens basieren alle auf einem rechtwinkligen Dreieck
Sie sind sehr ähnliche Funktionen … wir werden uns also die Sinusfunktion ansehen und dann den Sinus umkehren, um zu erfahren, worum es geht.,
Sinusfunktion
Der Sinus des Winkels θ ist:
- die Länge des seitlichen gegenüberliegenden Winkels θ
- geteilt durch die Länge der Hypotenuse
Oder einfacher:
sin(θ) = Entgegengesetzte / Hypotenuse
Die Sinusfunktion kann uns helfen, Dinge wie diese zu lösen:
Inverse Sinusfunktion
Aber manchmal ist es der Winkel, den wir finden müssen.
Hier kommt „Inverse Sine“ ins Spiel.
Es beantwortet die Frage „Welcher Winkel hat Sinus gleich gegenüber / Hypotenuse?,“
Das Symbol für inversen Sinus ist sin-1 oder manchmal arcsin.
Sie sind wie Vorwärts und rückwärts!

- sin nimmt einen Winkel und gibt uns das Verhältnis“Gegenteil/hypotenuse „
- sin-1 nimmt das Verhältnis“ Gegenteil/hypotenuse “ und gibt uns den Winkel.
Beispiel:
Rechner
 |
Auf dem Rechner drücken Sie eine der folgenden Tasten (abhängig von Ihrer Rechnermarke):entweder ‚2ndF sin‘ oder ’shift sin‘. |
Versuchen Sie auf Ihrem Rechner, sin und dann sin-1 zu verwenden, um zu sehen, was passiert
Mehr als ein Winkel!
Inverser Sinus zeigt nur einen Winkel an … aber es gibt mehr Winkel, die funktionieren könnten.
Beispiel: Hier sind zwei Winkel, wobei opposite / hypotenuse = 0.,5
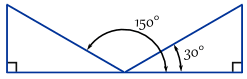
Tatsächlich gibt es unendlich viele Winkel, weil Sie 360°addieren (oder subtrahieren) können:
Denken Sie daran, denn es gibt Zeiten, in denen Sie tatsächlich einen der anderen Winkel benötigen!
Zusammenfassung
Der Sinus des Winkels θ ist:
sin (θ) = Opposite / Hypotenuse
Und inverser Sinus ist:
sin-1 (Opposite / Hypotenuse) = θ
Was ist mit “ cos „und“ tan „… ?
Genau die gleiche Idee, aber unterschiedliche Seitenverhältnisse.,
Kosinus
Der Kosinus des Winkels θ ist:
cos(θ) = Angrenzend / Hypotenuse
Und inverser Kosinus ist :
cos-1 (Benachbart / Hypotenuse) = θ
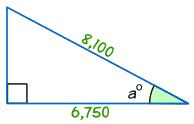
Beispiel: Finden Sie die Größe des Winkels a°
cos a° = Benachbarte / Hypotenuse
cos a° = 6,750/8,100 = 0,8333…
a° = cos-1 (0.8333…) = 33.,6° (bis 1 Dezimalstelle)
Tangente
Die Tangente des Winkels θ ist:
tan(θ) = Opposite / Adjacent
So Inverse Tangente ist :
tan-1 (Opposite / Adjacent) = θ
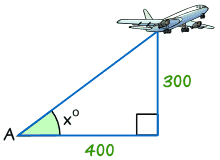
Beispiel: Finden die größe von winkel x°
tan x° = Gegenüber / Benachbarten
tan x° = 300/400 = 0,75
x° = tan-1 (0,75) = 36.,9° (korrekt auf 1 Dezimalstelle)
Andere Namen
Manchmal wird sin-1 asin oder arcsin genannt
Ebenso wird cos-1 acos oder arccos genannt
Und tan-1 heißt atan oder arctan
Beispiele:
- arcsin(y) ist das gleiche wie sin-1(y)
- atan(θ) ist das gleiche wie tan-1(θ)
- usw.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- Aber der umgekehrte Sinus und der umgekehrte Kosinus „gehen nicht für immer weiter“, wie es Sinus und Kosinus tun …
Schauen wir uns das Beispiel des Kosinus an.
Hier sind Kosinus und inverser Kosinus in demselben Diagramm dargestellt:
Kosinus und inverser Kosinus
Sie sind Spiegelbilder (ungefähr die Diagonale)
Aber warum wird der umgekehrte Kosinus oben und unten abgeschnitten (die Punkte sind nicht wirklich Teil der Funktion) … ?
Denn um eine Funktion zu sein, kann es nur eine Antwort geben
wenn wir fragen: „Was ist cos-1 (x) ?,“
Eine Antwort oder unendlich viele Antworten
Aber wir haben früher gesehen, dass es unendlich viele Antworten gibt, und die gepunktete Linie in der Grafik zeigt dies.
Also, ja, es gibt unendlich viele Antworten …
… aber stellen Sie sich vor, Sie geben 0.5 in Ihren Rechner ein, drücken cos-1 und es gibt Ihnen eine unendliche Liste möglicher Antworten …
Wir haben also diese Regel, dass eine Funktion nur eine Antwort geben kann.
Wenn wir es also so abschneiden, erhalten wir nur eine Antwort, aber wir sollten uns daran erinnern, dass es andere Antworten geben könnte.,
Tangente und inverse Tangente
Und hier ist die Tangens-Funktion und inverse Tangente. Können Sie sehen, wie sie Spiegelbilder sind (über die Diagonale) …?

Tangente

Inverse Tangente



