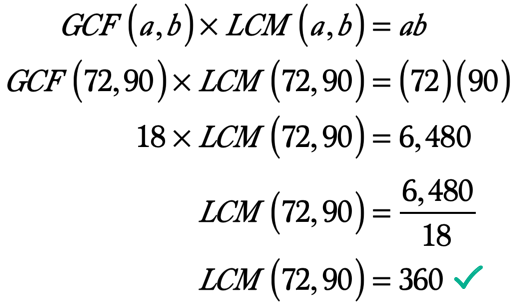Quando stavi studiando come trovare il GCF e LCM di due numeri positivi, hai scoperto una relazione molto interessante tra le due quantità?

L’ho fatto! In realtà l’ho scoperto per caso quando ero un giovane studente e pensavo di essermi imbattuto in qualcosa di “rivoluzionario”. Ero così eccitato che ho condiviso con il mio insegnante., Ma per la mia frustrazione, mi guardò negli occhi e disse che era già una dichiarazione matematica provata. Mi sono sentito scoraggiato per un momento, ma sono tornato al mio lavoro scolastico e ho continuato.

Se non l’hai ancora incontrato, c’è una notevole relazione algebrica o legame tra il più grande Fattore comune (GCF) e il Minimo Comune Multiplo (LCM) di due numeri. In questa lezione, i numeri che vogliamo sono quelli appartenenti solo all’insieme di numeri interi positivi.,
Di seguito è riportata la connessione algebrica tra GCF e LCM di due interi positivi.
La formula GCF-LCM
ATTENZIONE: non esiste davvero una cosa come la “Formula GCF-LCM”. Ho appena fatto il nome per facilità di riferimento. Si può chiamare tutto quello che vuoi fintanto che serve il suo scopo.,
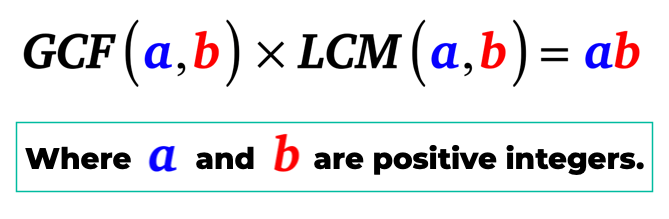
Semplicemente, il massimo comune divisore di a e b, quando moltiplicato per il minimo comune multiplo di a e b è uguale al prodotto di a e b. Che è, a e b sono interi positivi.
Problemi di esempio
Esempio 1: Il GCF di 12 e 16 è 4. Qual è il LCM di 12 e 16?
È possibile determinare LCM di 12 e 16 utilizzando uno dei due metodi seguenti.,
- Trovare LCM usando il metodo List
- Trovare LCM usando il metodo di fattorizzazione Prime
Tuttavia, c’è un modo molto più veloce. Puoi sfruttare la “Formula GCF-LCM” perché conosci i due interi e il suo GCF. Basta collegare i valori nella formula quindi risolvere per LCM.
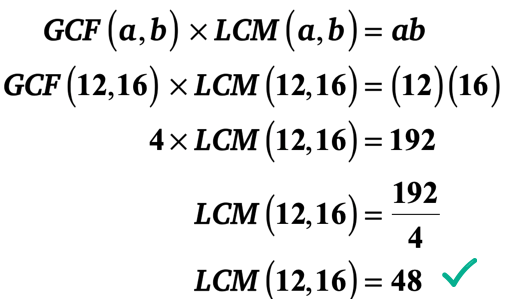
Lascerò a voi verificare che LCM di 12 e 16 sia effettivamente 48.
Esempio 2: LCM di 24 e 40 è 120. Qual è il GCF di 24 e 40?,
Questo problema è l’esatto opposto dell’esempio 1 perché ti viene dato il valore di LCM invece di GCF.
Quindi queste sono le informazioni che conosciamo. Descriviamoli per chiarezza.
▶︎ LCM(24,40) = 120
▶︎ a=24 e b=40 quindi ab = \left( {24} \right)\left( {40} \right) = 960
📌 Nota: Non importa quali numeri sono a e b. Non cambierà il risultato della risposta finale. Tuttavia, è una buona pratica standardizzare la soluzione. Suggerisco di lasciare a essere il numero intero più piccolo mentre b essere il numero intero più grande.,
Sostituiamo i valori noti nella formula quindi risolviamo per il GCF di 24 e 40.
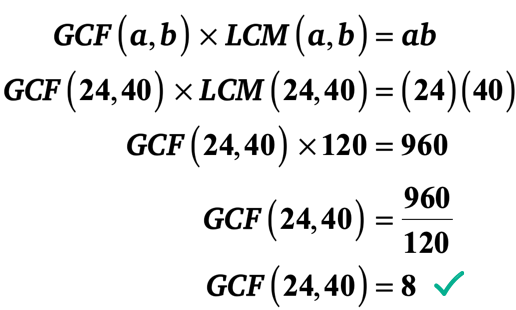
Esempio 3: Trovare il GCF di 20 e 25 calcolando prima il LCM di 20 e 25.
Questo problema sarà un po ‘ diverso dagli esempi #1 e #2. Dovrai calcolare prima il Minimo comune multiplo (LCM) di 20 e 25. Successivamente, è possibile risolvere il più grande fattore comune (GCF) di 20 e 25 utilizzando la formula GCF-LCM.
Quindi eccoci qui!, Per trovare il LCM di 20 e 25, scriveremo i primi multipli di 20 e 25. Il primo multiplo comune che si presenta sarà il nostro LCM.
Multipli di 20: 20, 40, 60, 80, 100, 120
Multipli di 25: 25, 50, 75, 100, 125, 150
Poiché il numero 100 si presenta come il primo multiplo comune di 20 e 25, allora possiamo affermare che LCM di 20 e 25 è 100.
Ora abbiamo tutte le informazioni per usare la formula. Di seguito sono riportati i valori che sostituiremo nella formula per risolvere per LCM di 20 e 25.,
◉ Il prodotto di a e b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ LCM di 20 e 25 → LCM\left( {20,25} \right) = 100
Ecco il calcolo per risolvere il GCF 20 e i 25 anni:
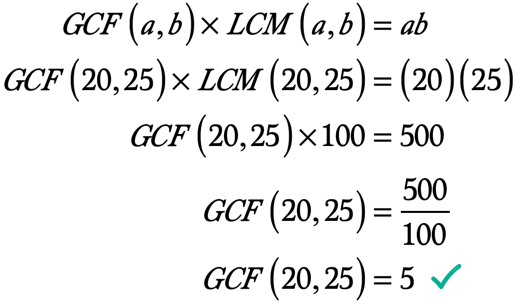
Esempio 4: Trovare il LCM di 63 84 mediante il calcolo del GCF di 63 e 84.
Questo problema è molto simile all’esempio #3. L’unica differenza è che calcolerai prima il GCF invece del LCM, come indicato dal problema stesso.,
Troviamo tutti i fattori di 63 e 84. È possibile utilizzare la tecnica “metodo arcobaleno” per calcolare i numeri interi dati.
Si noti che il fattore comune più grande o più alto tra i due elenchi è 21.
Fattori di 63: 1, 3, 7, 9, 21, 63
Fattori di 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Pertanto, il più Grande Fattore Comune, 63 84 21. Quindi, GCF \ left ({63,84} \ right) = 21.,
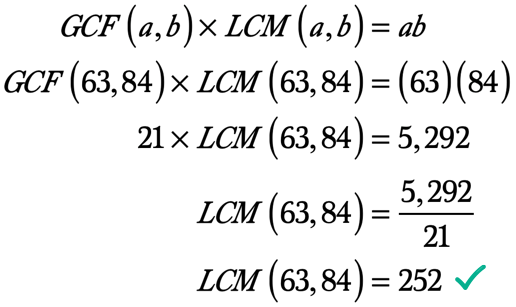
Esempio 5: Trovare il LCM di 72 e 90, utilizzando il GCF-LCM Formula.
Come già sappiamo, possiamo trovare LCM di due interi con il valore del suo GCF usando la Formula GCF-LCM.,
Elenco sia i fattori di 72 e 90, abbiamo:
Tutti i fattori di 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Tutti i fattori di 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Quando si confrontano le liste di fattori, vediamo che il 18 è il fattore che è comune a entrambi, ma è il più grande o più grande in valore. Significa che il GCF di 72 e 90 è 18, cioè GCF \ left ({72,90} \right) = 18.
Ora siamo pronti a sostituire i valori sottostanti nella formula.,
ab ab = \left( {72} \right)\left( {90} \right) = 6,480
G GCF\left( {72,90} \right) = 18
Ecco il calcolo per trovare l’LCM dato che conosciamo già il GCF dei due interi e il loro prodotto.