Sekvens
En Sekvens er et sett av ting (vanligvis tall) som er i orden.
Geometriske Sekvenser
I en Geometrisk Sekvens hver term er funnet ved å multiplisere den forrige term av en konstant.
Generelt kan vi skrive en Geometrisk Sekvens som dette:
{a, ar, ar2, ar3, …, }
hvor:
- en er den første termen, og
- r er den faktoren mellom begrepene (kalt «felles ratio»)
Men vær forsiktig, r burde ikke være 0:
- Når r=0, får vi sekvensen {a,0,0,…} som ikke er geometrisk
Regelen
Vi kan også beregne noe tid ved hjelp av Regelen:
xn = ar(n-1)
(Vi bruker «n-1» fordi ar0 er for 1. termin)
En Geometrisk Sekvens kan også ha mindre og mindre verdier:
Eksempel:
4, 2, 1, 0.5, 0.25, …,
Denne sekvensen har en faktor på 0,5 (en halv) mellom hvert tall.
Sine Regel er xn = 4 × (0.5)n-1
Hvorfor «Geometriske» Rekkefølge?,
Fordi det er som å øke dimensjonene i geometri:
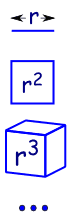 |
en linje er 1-dimensjonale og har en lengde på r |
| i 2 dimensjoner et kvadrat har et areal på r2 | |
| i 3 dimensjoner en kube som har volum r3 | |
| osv (ja, vi kan ha 4 og flere dimensjoner i matematikk)., |
Geometriske Sekvenser er noen ganger kalt Geometriske Progresjoner (G. P. ‘ s)
Summere en Geometrisk Serien
for Å oppsummere disse:
a + ar + ar2 + … + ar(n-1)
(Hver term er arken, hvor k starter på 0 og går opp til n-1)
Vi kan bruke denne praktiske formel:

– en er den første term
r er den «vanlige forholdet» mellom ordene
n er antall vilkår
Hva er så morsomt Σ symbol?, Det heter Sigma Notasjonen
| (kalt Sigma) betyr «oppsummere» |
Og nedenfor og ovenfor det vises start-og slutt-verdier:
Det står «Oppsummere n, hvor n går fra 1 til 4. Svar=10
formelen er enkel å bruke …, bare «plug in» verdiene av a, r og n
ved Hjelp av Formelen
La oss se på formelen på følgende:
Eksempel: Korn av Ris på Brettet

På siden Binære Sifre vi gi et eksempel på korn av ris på et sjakkbrett. Spørsmålet er spurt:
Når vi setter ris på brettet:
- 1 korn på den første plassen,
- 2 korn på den andre plassen,
- 4 korn på den tredje og så videre,
- …
… dobling korn av ris på hver firkant …
…, hvor mange korn av ris totalt?
Slik at vi har:
- a = 1 (første periode)
- r = 2 (dobler hver gang)
- n = 64 (64 rutene på brettet)
Slik:

Blir:
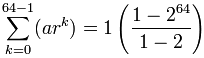
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
Som var akkurat det resultatet vi fikk på de Binære Sifrene side (takk og lov!)
Og et annet eksempel, denne gang med r mindre enn 1:
Hvorfor Gjør Formelen Fungerer?,
La oss se hvorfor formelen fungerer, fordi vi kommer til å bruke et interessant «triks» som er verdt å vite.
legg Merke til at S og S·r er lik?
Nå trekke fra dem!
Wow! Alle vilkårene i midten pent kansellere ut.,
(Som er et godt triks)
Ved å trekke fra S·r fra S vi få et enkelt resultat:
S − S·r = a − arn
La oss omorganisere det å finne S:
Som er vår formel (ta-da!):

Uendelig Geometrisk Serien
Så hva skjer når n går mot evigheten?,
Vi kan bruke denne formelen:
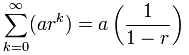
Men vær forsiktig:
r må være mellom (men ikke inkludert) -1 og 1
og r burde ikke være 0 fordi sekvensen {a,0,0,…} er ikke geometriske
Så vår infnite geometriske serien har en begrenset sum når forholdet er mindre enn 1 (og større enn -1)
La oss få tilbake våre tidligere eksempel, og se hva som skjer:
|
tror du ikke på meg? Bare se på denne plassen: Ved å legge opp 12 + 14 + 18 + … vi ender opp med hele greia!, |
 |
Periodiske Desimaltall
På en annen side, spurte vi «Gjør 0.999… lik 1?»vel, la oss se om vi kan beregne det:



