Hva er termisk ekspansjon?
Termisk ekspansjon er fenomenet hvor et objekt eller kroppen utvider seg i reaksjon til å bli oppvarmet. Termisk ekspansjon er mest åpenbart i gasser og væsker, men kan likevel ha en betydelig effekt på tørrstoff.

Figure1: togskinner bøyd på grunn av lineær termisk utvidelse
Den termiske egenskaper av en solid er et veldig viktig aspekt i utformingen av fabrikker og produkter., Hvis termisk ekspansjon er ikke vurdert under konstruksjon og design, resultatet kan være store strukturelle skader i en maskin eller en bygning. Utallige tiltak har vært iverksatt for å hindre dette og mange smarte teknologier som er utviklet for å stole på dette fenomenet. Beløpet som en materialet utvider seg kan forklares ved å vurdere en koeffisient som svarer til brøk vekst av materialet per grad endring i temperatur. Denne koeffisienten er kalt koeffisient av termisk utvidelse og brukes til å forutsi vekst av materialer i respons til en kjent temperaturen endres., Jo større denne koeffisienten er for et materiale, jo mer vil det utvide per grad temperaturøkning.
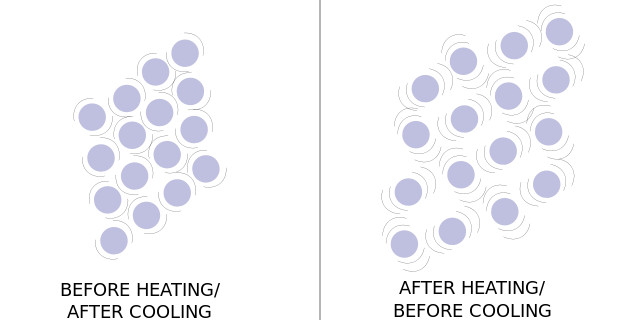
Figur 2: skjematisk fremstilling av atomic vibrasjoner før og etter oppvarming.
Når kroppen er oppvarmet, det er å akseptere og lagring av energi i atomer i form av kinetisk energi. Dette utsett til økt temperatur fører til et atom er naturlige vibrasjoner for å vokse sterkere og mer markert., Denne økningen i vibrasjon presser mot inter-molekylære krefter, slik at atomer eller molekyler til å bli lenger fra hverandre og kroppen til å vokse seg større. Det beløp som et stoff utvider seg i reaksjon på en endring i temperatur er matematisk representert ved en koeffisient av termisk ekspansjon. Denne koeffisienten er unike for hvert materiale og er basert på deres andre fysiske egenskaper. Jo høyere koeffisient av termisk ekspansjon materiale har, jo mer vil det ekspandere i reaksjon til å bli oppvarmet., Krystaller har en tendens til å ha den laveste termisk ekspansjon koeffisienter fordi deres struktur er svært ensartet og strukturelt lyd. Diamond har den laveste kjent termisk ekspansjonskoeffisient av alle naturlig forekommende materialer. Den faste stoffer med høyeste koeffisienter av termisk ekspansjon er de som har svak inter-molekylær obligasjoner, vanligvis polymerer, som også har en tendens til å ha lave smelte poeng. Grunnen til dette er at svakere bindinger er overvunnet med mindre vibrerende energi., Metaller har en tendens til å ha relativt lave koeffisienter, men de har også svært høy smelte poeng, og de er ikke så merkbar for en vesentlig feil forårsaket av stress ekspansjon. Dette gjør metaller ideelle kandidater til bruk ved måling av termisk ekspansjon.
Målinger av en endring i volum forårsaket av en fysisk eller kjemisk prosess som kalles dilatometry. Et instrument utviklet for å måle endring i volumet av noen stoffer som kalles en dilatometer., Det vanligste eksempelet på en dilatometer er en mercury termometer som måler volum og endring i volumet på fanget kvikksølv som er brukt for å bestemme temperaturen i omgivelsene. Dilatometers kan også brukes til å beregne koeffisient av termisk ekspansjon. For å finne ut koeffisient, volumet av materialet er nøye målt som temperaturen stiger fra en kjent verdi til en annen. Det er et par eksempler på dilatometers som er designet for å måle volumet av solid metall stykker for å avgjøre termisk ekspansjon., En design er kapasitans dilatometers. I denne designen, en plate av en kondensator er bevegelig, og prøven er plassert bak det, så når det utvider det skyver bevegelig plate nærmere den andre platen. En mer moderne og nøyaktig eksempel ville være laser dilatometer, som hele tiden måler dimensjoner for eksempel med lasere. En av de mest allsidige design er den optiske dilatometer som er rett og slett et digitalt kamera ved hjelp av en optisk gruppe for å måle variasjoner i utvalget størrelse.,
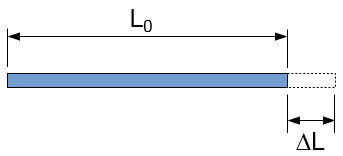
Figur 3: diagram som viser effekten av lineær termisk ekspansjon.
Gasser og væsker alltid utvide volumetrically, utvide innenfor rammen av sine beholdere. I teorien, tørrstoff alltid utvide volumetrically så godt, men fordi de holder formen deres og det gjør dem synes å utvide seg annerledes. For eksempel, når en lang metall stang som er oppvarmet atomer reise lenger fra hverandre i alle tre dimensjoner. I løpet av denne utvidelsen, stenger cross-sectional vekst vil neppe være merkbart i forhold til sin vekst på langs., Siden stangen er i utgangspunktet svært tynn, det er et relativt lite antall atomer presser mot hverandre i cross-sectional retning. I langsgående retning, men det er et større antall atomer stilt opp, og når de alle presse mot hverandre danner en kjede reaksjon som presser den totale lengden av stangen til å være mye større enn det var.
Objekter med dimensjoner som kan dette betraktes som bare vokser i en dimensjon. De er antatt å ha en koeffisient av lineær termisk ekspansjon i stedet for en koeffisient av volum termisk ekspansjon., Denne koeffisienten fungerer det samme som de tre-dimensjonale koeffisient av ekspansjon, bortsett fra at det svarer til brøk økning i lengde (i stedet for volum) per graders temperatur. Det samme er sant om koeffisientene i området ekspansjon i to dimensjoner for flate plater. Fra denne observasjonen det kan bestemmes at beløpet som kroppen utvider seg i respons til en økning i temperatur er lineært avhengig av den opprinnelige størrelsen av kroppen.
En observerende tilnærming kan være vedtatt å finne et nyttig ligningen til å forutsi noe som resulterer størrelse av en kropp etter en temperaturendring., Som forklart over, er det beløp som en lineær stoff utvider er lineært relatert til den opprinnelige lengde, (L0). Observasjon viser at utvidelsen er også omtrent lineært relatert til endringen i temperatur (dT). Det er også klart gjennom observasjon at alle materialer utvide annerledes. På grunn av denne variasjonen i ekspansjon mønstre, kan det bestemmes at andre fysiske aspekter innflytelse termisk ekspansjon. En koeffisient er brukt til å redegjøre for om et stoff er andre fysiske egenskaper. Denne koeffisienten er kjent som koeffisient av lineær termisk ekspansjon, (α)., Ligningen for den endelige lengde vil derfor være
L = L0 + L0*α*dT
Som kan være re arrangert for α
α = (L – L0)/(L0*dT)
Eller om det er sagt at endringer i lengde, L – L0, er dL
α = 1/L0 * dL/dT
Den samme logikken kan brukes til å bygge ligninger om volum-utvidelsen. De er like, bortsett fra lengden variabel ville være byttet for volum og lineær ekspansjonskoeffisient ville bli endret til volumetrisk. For å sikre nøyaktighet, er det ideelt å utlede volum utvidelse ligningen fra den lineære ligningen.,
V = L3 = 3
Fra analyser ved hjelp av den lineære metode, det er tydelig at verdien av α er vanligvis i deler per million rekkevidde (x10-6). Siden verdien er så liten, både de vilkår som heve den til en makt over ett resultat i en så liten verdi at de har nesten ingen effekt på resultatet. Disse vilkårene kan bli oversett av tilnærmet litt.
V = L03
= V0
Siden α er en konstant ukjent koeffisient, kan det sies at 3α er en ny konstant ukjent koeffisient som heter koeffisient av volum termisk ekspansjon, (β).,
V = V0 + V0*β*dT
β = 1/V0 * dV/dT
Denne formen for ligningen kan nå brukes til å finne koeffisienter av termisk ekspansjon av materialer etter å måle dem med en dilatometer over en kjent temperaturen endres. Disse likningene viser at både lineære og volum utvidelse omregningsfaktorer enheter av Kelvin-1, Celsius-1, eller Fahrenheit-1.
Med en dilatometer og et termometer, det er veldig rett frem for å utføre et eksperiment på et utvalg, og deretter følger ligningen for å beregne termisk ekspansjon koeffisienter., Aluminium er et praktisk materiale for å studere med denne metoden, som det har en svært høy ekspansjonskoeffisient for et metall. Rustfritt stål er kanskje den mest vanligvis målt på grunn av sin overflod av bruk i mange applikasjoner. Disse stål har en koeffisient som er omtrent gjennomsnittet for metaller, men de er ikke svært verdifull som sølv og gull. Mangel på termisk kunnskap i løpet av engineering og design kan resultere i kollaps av broer eller ødeleggelse av verdifullt utstyr., Den termiske utvidelsen av materialer som kan være en stor hindring for å bygge og designe, imidlertid, mange program prosesser og teknologi som har blitt designet med termisk ekspansjon som en fundamental komponent av funksjon.

Figur 4: ekspansjonsfuge på en bro
