Den enkleste måten å fange ideen om en voksende befolkning med et enkelt encellede organismen, for eksempel en bakterie eller et cilliate. I Figur 1, en befolkning på Paramecium i et lite laboratorium depresjon skyv er avbildet. I denne gruppen av individer som deler én gang per dag. Så, som starter med et enkelt individ på dag 0, forventer vi, i påfølgende dager, 2, 4, 8, 16, 32, og 64 individer i befolkningen., Vi kan her se at på en bestemt dag, antall personer i befolkningen er rett og slett to ganger hva tallet var dagen før, slik at antallet i dag, kaller det N(i dag), er lik det dobbelte av antallet i går, kall det N(i går), som vi kan skrive mer kompakt som N(i dag) = 2N(i går).
Så er det fornuftig å skrive dette som, N(t) = 2N(t – 1) der t kunne ta på noen verdi i det hele tatt.,
Nå kan vi generalisere denne ideen en litt hvis vi oppmerksom på at på dag seks antallet er lik to ganger antall på dag fem, eller N(6) = 2N(5) og i dag fem antallet er lik to ganger antall på dag fire, eller N(5) = 2N(4), osv.
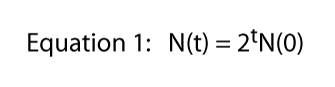
hvor t står for noe tid i det hele tatt (for eksempel, hvis t = 6, N(6) = 26).
Endelig har vi oppmerksom på at denne ligningen ble avledet fra den konkrete situasjonen vist i Figur 1, hvor en divisjon per dag var harde og raske regler., Det er der 2 kommer fra i Ligning 1 — fra hver enkelt Paramecium vi får to individer neste dag. Selvfølgelig divisjon pris kunne være noe. Hvis det var to divisjoner per dag, men én celle alltid døde, ville vi forvente tre personer fra hvert enkelt individ og Ligning 1 ville være N(t) = 3tN(0)., Så divisjonen pris kan være noe antall i det hele tatt og den generelle ligningen blir,
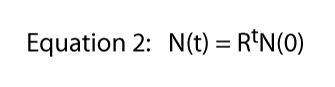
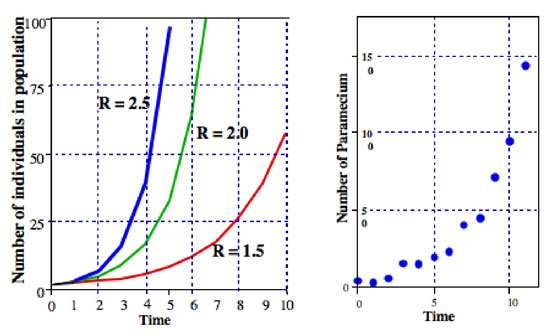
hvor R er vanligvis kalles den endelige pris av befolkningen øker (i aktuell sak for å dele Paramecium den endelige pris av befolkningen økningen er lik divisjon pris). I Figur 2 har vi illustrere denne ligningen for ulike verdier av R. Det er vanligvis referert til som den eksponentielle ligningen, og i form av dataene i Figur 2 er den generelle formen kalles eksponentiell.,
Enhver verdi av R kan være representert i et uendelig antall måter (for eksempel, hvis R = 16, vi kan skrive R = 8 x 2, eller R = 42, eller R = 32/2, eller R = 2.718282.77). Det siste uttrykket (R = 2.718282.,77) gjør bruk av en viktig konstant som kan hentes fra elementær analyse, Euler ‘ s konstant. Å uttrykke hva verdien av R som Euler ‘ s konstant hevet til noen makt er faktisk svært nyttig — det gir full effekt av kalkulus inn i bildet.,olize Euler ‘ s konstant som e kan vi skrive Ligning 2
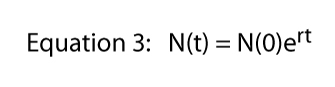
Nå, hvis vi tar den naturlige logaritmen av begge sider av Ligning 3 — husk ln(ex) = x — Ligning 3 blir: ln = ln + rt
Og hvis vi begynte befolkningen med en enkelt person (som i eksempelet ovenfor), vi har

som vi ser at den naturlige logaritmen av befolkningen, til enhver tid, er noen konstant, ganger at tid., Konstant r er referert til som den reelle pris for naturlig tilvekst (Figur 2).
Alle slags mikroorganismer utstilling mønstre som er svært nær eksponentiell befolkningsvekst. For eksempel, i det høyre diagrammet i Figur 2 er en befolkning på Paramecium vokser i et laboratorium kultur. Mønster av vekst er svært nær mønster av den eksponentielle ligningen.
en Annen måte å skrive den eksponentielle ligningen er som en differensial-ligningen, som er, som representerer vekst i befolkningen i sin dynamiske form., Heller enn å spørre hva som er størrelsen på befolkningen ved tid t, spør vi, hva er hastigheten som befolkningen vokser ved tid t. Prisen er symbolisert som dN/dt som rett og slett betyr «endring i N i forhold til endring i t», og hvis du husker din grunnkurs i analyse, kan vi finne vekstrate ved å skille Ligning 4, som gir oss
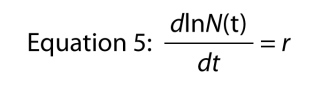
som er en slags bemerkelsesverdig, fordi det sier at veksten i loggen for antall i befolkningen er konstant., Som konstant vekst av loggen av befolkningen er den iboende om økningen.,
Husker at endring av logaritmen til et tall er det samme som «per capita» endring i dette nummeret, noe som betyr at vi kan skrive Ligning 5 som

hvor vi utelate variabelen t fordi det er åpenbart hvor det går, og så skal vi ordne litt til å komme opp med
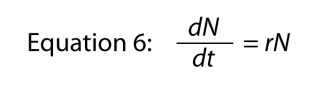
hvor parameteren r, igjen, iboende pris av naturlig tilvekst., Det grunnleggende forholdet mellom finitte om økningen og iboende pris er
r = ln(R)
hvor ln refererer til den naturlige logaritmen. Merk at Ligning 6 og Ligning 3 er bare forskjellige former av samme likningen (Likning 3 er integrert form av Ligning 6; Ligning 6 er differensiert form av Ligning 3), og begge kan bli referert til som den eksponentielle ligningen.,

Den eksponentielle ligningen er en nyttig modell av enkle bestander, i hvert fall for relativt korte perioder av gangen., For eksempel, hvis et laboratorium tekniker trenger å vite når en bakteriekultur når en viss befolkningstetthet, den eksponentielle likningen kan brukes til å gi en prediksjon som nøyaktig når som bestandsstørrelse vil bli nådd. Et annet eksempel er i tilfelle landbruket skadedyr. Planteetere er alltid potensielt store problemer for planter. Når plantene utsatt for slike utbrudd er landbruket, som er å si avlinger, tap kan være veldig viktig for både bonde og forbruker. Dermed, det er alltid press for å hindre at slike utbrudd., Siden andre VERDENSKRIG er den viktigste våpen i kampen mot slike skadedyr utbrudd har vært kjemiske plantevernmidler, for eksempel DDT. Men i de senere årene har vi kommet til å innse at disse plantevernmidler er ekstremt farlig på lang sikt, både for miljøet og for folk. Følgelig har det vært en bevegelse for å begrense mengden av plantevernmidler som er sprayet for å bekjempe skadedyr. Den viktigste måten dette er gjort på, er å etablere en økonomisk terskel, som er befolkningstettheten av potensielle skadedyr nedenfor som skade på avling er ubetydelig (dvs., det er egentlig ikke nødvendig å sprøyte)., Når pest befolkningen øker over terskelen, bonden behov for å iverksette tiltak og anvende noen form av plantevernmiddel, eller andre verktøy for å kontrollere skadedyr. Gitt arten av dette problemet, noen ganger er det av største betydning for å være i stand til å forutsi når pest vil nå økonomisk terskel. Å vite R for pest arter kan bonden til å forutsi når det vil være nødvendig å bruke noen form for kontroll prosedyre (Figur 3).
Den eksponentielle ligningen er også en nyttig modell for å utvikle intuitive ideer om bestander., Det klassiske eksempelet er et tjern med en befolkning på lily pads. Hvis hver lily pad reproduserer seg selv (to pads ta plassen hvor en pad hadde vært) hver måned, og det tok, la oss si, tre år for dammen til å bli halvparten fylt med lily pads, hvor mye lenger tid vil det ta for dammen for å være helt dekket med lily pads? Hvis du ikke slutte å tenke for klart det er fristende å si at det vil ta like mye tid som tre år, for andre halvdel av dammen til å bli så fylt som den første. Svaret, selvfølgelig, er en måned.,
en Annen populær eksempel er den velkjente gamle Egyptiske (eller noen ganger persiske) matematiker som ber om betaling fra kongen i form av korn av hvete (noen ganger ris). En korn på den første plassen på brettet, to korn på den andre plassen, og så videre, helt til den siste plassen. Farao ikke kan forestille seg at en så enkel betaling kan beløpe seg til mye, og er så enig. Men han gjorde ikke fullt ut sette pris på eksponentiell vekst., Siden det er 64 rutene på brettet, kan vi bruke Ligning 2 for å finne ut hvor mange korn av hvete vil bli pålagt å betale på den siste plassen (R hevet til den 64. kraft, som om 18,446,744,074,000,000,000 — mye av hvete ja, sikkert mer enn i hele riket). Disse eksemplene understreker ofte overraskende måte som en eksponentiell prosessen kan føre til svært store tall svært raskt.
