Raskt Svar:
For en rettvinklede trekanten:

sinus-funksjon synd tar vinkel θ og gir forholdet motsatt hypotenuse
invers sinus-funksjon synd-1 tar forholdet oppositehypotenuse og gir vinkel θ
Og cosinus og tangens følge en lignende idé.,
Og nå for detaljer:
Sinus, Cosinus og Tangens er alle basert på en rettvinklede Trekanten
De er svært like funksjoner … så vil vi se på Sinus-Funksjonen, og deretter Invers Sinus til å lære hva det er alt om.,
Sinus-Funksjon
Sinus av en vinkel θ er:
- lengden på Motsatt side vinkel θ
- dividert med lengden av Hypotenuse
Eller enklere:
sin(θ) = Motsatte / Hypotenuse
Sinus-Funksjonen kan hjelpe oss med å løse ting som dette:
Invers Sinus-Funksjon
Men noen ganger er det vinkelen vi trenger å finne.
Dette er hvor «Invers Sinus» kommer inn.
Det svar på spørsmålet «hvilken vinkel har sinus lik motsatt/hypotenuse?,»
symbolet for invers sinus er synd-1, eller noen ganger arcsin.
De Er Som Fremover og Bakover!

- synd tar en vinkel, og gir oss forholdet motsatt/hypotenuse»
- synd-1 tar forholdet motsatt/hypotenuse» og gir oss vinkel.
Eksempel:
Kalkulator
 |
På kalkulatoren du trykker på en av følgende (avhengig av merke av kalkulator):enten ‘2ndF synd» eller «shift synd». |
På kalkulatoren, kan du prøve å bruke synd og deretter synd-1 å se hva som skjer
Mer Enn Én Vinkel!
Invers Sinus bare viser én vinkel … men det er flere vinkler som kan jobbe.
Eksempel: Her er to vinkler der motsatte/hypotenuse = 0.,5
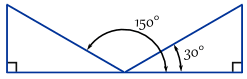
faktisk det er uendelig mange vinkler, fordi du kan fortsette å legge til (eller trekke) 360°:
Husk dette, fordi det er tider når du faktisk trenger en av de andre vinkler!
Oppsummering
Sinus av en vinkel θ er:
sin(θ) = Motsatte / Hypotenuse
Og Invers Sinus er :
synd-1 (Motsatt / Hypotenuse) = θ
Hva Om «cos» og «tan» … ?
Akkurat den samme ideen, men annen side forholdstall.,
Cosinus
Cosinus til vinkelen θ er:
cos(θ) = Tilstøtende / Hypotenuse
Og Invers Cosinus er :
cos-1 (Tilstøtende / Hypotenuse) = θ
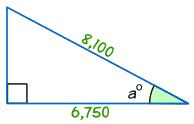
Eksempel: Finne størrelsen på en vinkel°
cos a° = Tilstøtende / Hypotenuse
cos a° = 6,750/8,100 = 0.8333…
a° = cos-1 (0.8333…) = 33.,6° (1 desimal)
Tangent
Tangent av vinkelen θ er:
tan(θ) = Motsatte / Tilstøtende
Så Invers Tangens er :
tan-1 (Motsatt / ved siden av) = θ
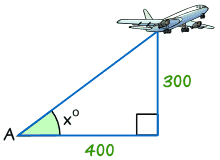
Eksempel: Finn størrelsen på vinkelen x°
tan x° = Motsatte / Tilstøtende
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (riktig til 1 desimal)
Andre Navn
noen Ganger synd-1 heter asin eller arcsin
på samme måte cos-1 kalles acos eller arccos
Og tan-1 kalles atan eller arctan
Eksempel:
- arcsin(y) er det samme som synd-1(y)
- atan(θ) er det samme som tan-1(θ)
- osv.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- Men Invers Sinus og Invers Cosinus-ikke «gå på for alltid» som Sinus og Cosinus gjøre …
La oss se på eksempel på Cosinus.
Her er Cosinus og Invers Cosinus plottet i samme diagram:
Cosinus og Invers Cosinus
De er speilbilder (om diagonalen)
Men hvorfor gjør Invers Cosinus få hugget av på toppen og bunnen (prikkene er ikke egentlig en del av-funksjon) … ?
Fordi å være en funksjon, kan den bare gi ett svar
når vi spør «hva er cos-1(x) ?,»
Ett Svar eller Uendelig Mange Svar
Men vi så tidligere at det finnes uendelig mange svar, og den stiplede linjen på grafen viser dette.
Så ja, det finnes uendelig mange svar …
… men tenk deg at du skriver 0.5 inn på kalkulatoren, trykker du cos-1, og det gir deg en uendelig liste av mulige svar …
Slik at vi har denne regelen for at en funksjon kan bare gi ett svar.
Så, ved å kutte det ut som at vi får bare ett svar, men vi må huske på at det kan være andre svar.,
Tangent og Invers Tangens
Og her er tangens-funksjonen og invers tangens. Kan du se hvordan de er speilbilder (om diagonalen) …?

Tangent

Invers Tangens



