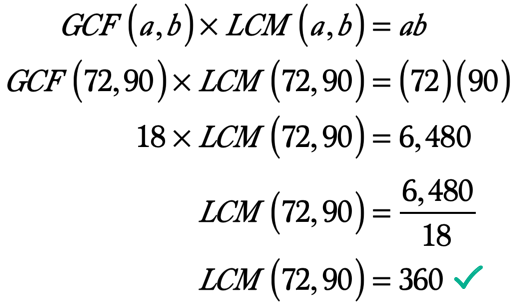Når du studerte hvordan finne GCF og LCM av to positive tall, gjorde du oppdage et veldig interessant forhold mellom de to mengder?

jeg gjorde! Jeg faktisk oppdaget det ved en tilfeldighet da jeg var en ung student, og jeg trodde jeg snublet over noe som var «revolusjonerende». Jeg var så spent at jeg delte det med læreren min., Men til min frustrasjon, han så meg inn i øynene og sa at det var allerede en bevist matematisk utsagn. Jeg følte meg motløs for et øyeblikk, men jeg gikk tilbake til min skole arbeid og presset på.

Hvis du ikke har oppdaget det ennå, det er en bemerkelsesverdig algebraiske forhold eller en kobling mellom de Største Felles Faktor (GCF) og Minste Felles Multiplum (LCM) av to tall. I denne leksjonen, de tallene som vi ønsker, er de som hører til settet av positive heltall bare.,
Nedenfor er algebraisk sammenheng mellom GCF og LCM av to positive heltall.
GCF-LCM Formel
ADVARSEL: Det er virkelig ikke noe slikt som «GCF-LCM Formel». Jeg har nettopp laget opp navnet for enkel referanse. Du kan kalle det hva du vil så lenge det tjener sin hensikt.,
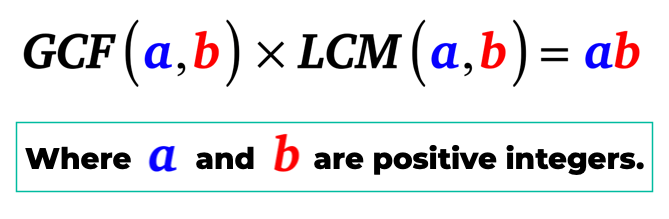
Enkelt sagt, den største felles faktor for a og b når multiplisert til minste felles multiplum av a og b er lik produktet av a og b. At a og b er positive heltall.
Eksempel Problemer
Eksempel 1: GCF 12 og 16 år er 4. Hva er LCM 12 og 16 år?
Du kan bestemme LCM 12 og 16 år ved hjelp av en av metodene nedenfor.,
- å Finne LCM ved hjelp av Listen Metode
- å Finne LCM ved hjelp av Prime Primtallsfaktorisering Metode
Men det er en mye raskere måte. Du kan dra nytte av «GCF-LCM Formel» fordi du kjenner to heltall og dens GCF. Bare plugg inn verdiene i formelen deretter løse for LCM.
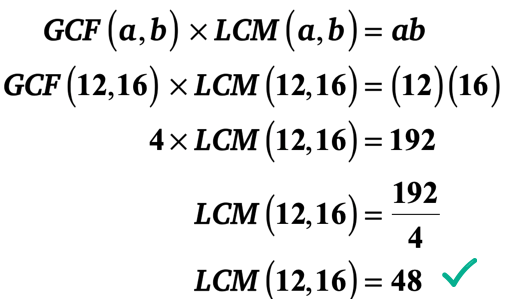
jeg vil la det til deg for å bekrefte at LCM 12 og 16 år er faktisk 48.
Eksempel 2: LCM av 24 og 40 120. Hva er GCF av 24 og 40?,
Dette problemet er det motsatte av Eksempel 1 fordi du er gitt verdien av LCM i stedet for GCF.
Så dette er informasjon som vi vet. La oss spesifisere dem for klarhet.
▶︎ LCM(24,40) = 120
▶︎ a=24 og b=40 derfor ab = \left( {24} \right)\left( {40} \right) = 960
📌 Merk: Det spiller egentlig ingen rolle hvilket tall er a og b. Det vil ikke endre utfallet av den endelige svar. Men, det er en god praksis å standardisere din løsning. Jeg foreslår at du lar en være mindre heltall, mens b være større heltall.,
La oss erstatte de kjente verdiene i formelen deretter løse for GCF av 24 og 40.
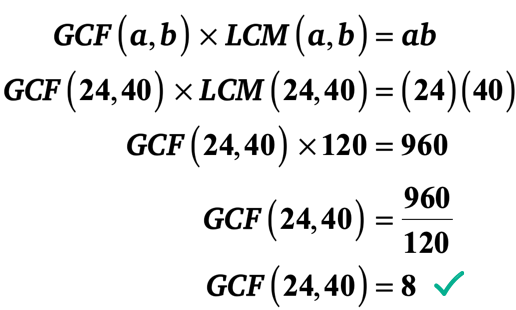
Eksempel 3: Finn GCF 20 og 25 ved først å beregne LCM 20 og 25.
Dette problemet vil være litt forskjellig fra eksempler #1 og #2. Du vil trenger for å beregne første Minste Felles Multiplum (LCM) 20 og 25. Etter det, kan du løse for den Største Felles Faktor (GCF) 20 og 25 ved hjelp av GCF-LCM Formel.
Så her går vi!, For å finne LCM 20 og 25, vil vi skrive de første få multispill på 20 og 25. Den aller første felles multiplum som vises vil være vår LCM.
Multipler av 20: 20, 40, 60, 80, 100, 120
Multipler av 25: 25, 50, 75, 100, 125, 150
Siden antall 100 dukker opp som den første felles multiplum av 20 og 25, så vi kan hevde at LCM 20 og 25 er 100.
nå har Vi all informasjon for å bruke formelen. Nedenfor er verdiene som vi kommer til å erstatte inn i formelen for å løse for LCM 20 og 25.,
◉ produktet av a og b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ Den LCM 20 og 25 → LCM\left( {20,25} \right) = 100
Her er beregningen for å løse for GCF 20 og 25:
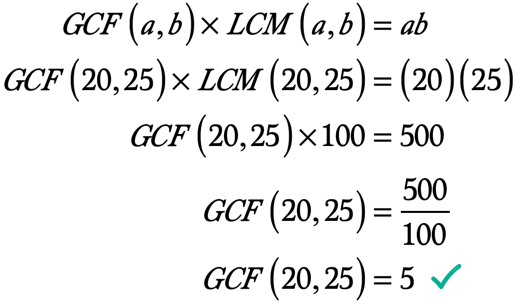
Eksempel 4: Finn LCM av 63 og 84 ved først å beregne GCF av 63 og 84.
Dette problemet er svært lik eksempel #3. Den eneste forskjellen er at du vil beregne først GCF i stedet for LCM, som instruert av problemet i seg selv.,
La oss finne alle faktorer av 63 og 84. Du kan bruke «rainbow metode» teknikk for å faktoren gitt heltall.
legg Merke til at den største eller høyeste felles faktor mellom de to listene er 21.
Faktorer av 63: 1, 3, 7, 9, 21, 63
Faktorer av 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Derfor, den Største Felles Faktor på 63 og 84 er 21. Dermed GCF\left( {63,84} \right) = 21.,
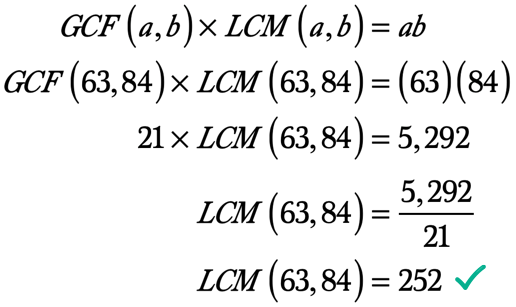
Eksempel 5: Finn LCM av 72 og 90 bruke GCF-LCM Formel.
Som vi allerede vet, kan vi finne LCM av to heltall med verdien av sin GCF bruke GCF-LCM Formel.,
Liste begge faktorene 72 og 90, har vi:
Alle faktorer av 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Alle faktorer av 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Når vi sammenligner lister over faktorer, ser vi at 18 er den faktor som er felles for begge, men har det største eller størst i verdi. Det betyr GCF av 72 og 90 er 18, det er, GCF\left( {72,90} \right) = 18.
Vi er nå klar til å erstatte verdiene nedenfor i formelen.,
❖ ab = \left( {72} \right)\left( {90} \right) = 6,480
❖ GCF\left( {72,90} \right) = 18
Her er regnestykket for å finne LCM gitt at vi vet allerede GCF av to heltall og deres produkt.