Etter å ha bygget en maskin læringsmodell, neste trinn er å evaluere modellen ytelse og forstå hvor bra vår modell er mot en referanseindeks modell., Evalueringen verdi som skal brukes vil avhenge av type problem du prøver å løse, enten det er en overvåket eller uten tilsyn problem, og hvis det er en klassifisering eller en regresjon oppgave.
I dette innlegget skal jeg snakke om to viktige evaluering verdiene som brukes for regresjon problemer og markere den største forskjellen mellom dem.
R-squared, også kjent som koeffisient besluttsomhet, definerer graden av variansen i den avhengige variabelen (eller mål) kan forklares av de uavhengige variable (funksjoner).,
La oss forstå dette med et eksempel — å si at den R-kvadrerte verdien for en bestemt modell kommer ut til å bli 0.7. Dette betyr at 70% av variasjonen i den avhengige variabelen forklares av de uavhengige variablene.
Ideelt sett ville vi ønsker at de uavhengige variablene er i stand til å forklare all variasjon i mål variabel. I dette tilfellet, den r-kvadrerte verdien ville være 1. Dermed kan vi si at høyere r-kvadrerte verdien, bedre i modellen.,
Så, i enkle termer, høyere R-squared, mer variasjon kan forklares med dine innspill variabler og dermed bedre er modellen. Også, den r-kvadrerte vil variere fra 0 til 1. Her er formelen for beregning R-squared-
R-squared er beregnet ved å dele summen av kvadratene av restprodukter fra regresjonsmodellen (gitt av SSres) av summen av kvadratene av feil fra gjennomsnittlig modell (gitt av SStot) og deretter trekke det fra 1.,
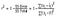
En ulempe av r-squared er at det forutsetter at hver variabel bidrar til å forklare variasjonen i mål, noe som kanskje ikke alltid være sann. For eksempel, hvis vi legge til en nye funksjoner for data (som kan eller ikke kan være nyttig), den r-kvadrerte verdien for modellen vil enten øke eller opprettholde samme, men det ville aldri nedgang.
Dette er tatt vare på av en litt modifisert versjon av r-squared, kalt justert r-kvadrert.,
Justert R-kvadrert
Lik R-squared, Justert R-kvadrat måler variasjonen i den avhengige variabelen (eller mål), forklares med bare funksjoner som er nyttig i å gjøre spådommer. I motsetning til R-squared, Justert R-kvadrert ville straffe deg for å legge til funksjoner som ikke er nyttig for å forutsi målet.
La oss matematisk forstå hvordan denne funksjonen er innkvartert i Justert R-Kvadrert., Her er formelen for justert r-kvadrert

Her R^2 r-squared beregnet, N er antall rader og M er antall kolonner. Som nummer av funksjonen øker verdien i nevneren synker.
- Hvis R2 øker med en betydelig verdi, og deretter justert r-kvadrert ville øke.
- Hvis det er noen betydelig endring i R2, så den justerte r2 ville avta.
