Statistikk 2 – korrelasjonskoeffisienten og determinasjonskoeffisient

korrelasjonskoeffisient

Hvor godt gjør din regresjonsligningen virkelig representerer
settet av data?
En av måtene å finne ut svaret på dette spørsmålet er å
eksamen korrelasjonskoeffisienten og determinasjonskoeffisient.,

mengde r, kalt lineær korrelasjon koeffisient, måler styrke og
retning av en lineær sammenheng mellom to variabler. Den lineære sammenhengen
– koeffisienten er noen ganger referert til som Pearson produkt moment korrelasjon koeffisient i
ære for sin utbygger Karl Pearson.
Den matematiske formelen for computingr er: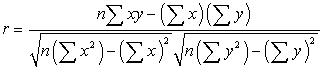

der n er antall par av data.,
(Er du ikke glad for at du har en grafisk kalkulator som regner ut denne formelen?)
verdien av r er slik at -1 < r < +1. + Og – tegn er brukt for positive
– lineære sammenhenger og negative lineære sammenhenger, henholdsvis.
Positiv korrelasjon: Hvis x og y har en sterk positiv lineær korrelasjon,r er nær
til +1. En r-verdi på nøyaktig +1 indikerer en perfekt positiv passform., Positive verdier
indikere en sammenheng mellom x-og y-variabler, slik som som verdier for x øker,
verdiene for y også øke.
Negativ korrelasjon: Hvis x og y har en sterk negativ lineær korrelasjon,r er nær
-1. En r-verdi på nøyaktig -1 indikerer en perfekt negativ passform. Negative verdier
indikere en sammenheng mellom x og y slik at som verdier for x øker, verdier
for y reduseres.
Ingen korrelasjon: Hvis det ikke er noen lineær sammenheng eller en svak lineær korrelasjon, r
nær 0., En verdi nær null betyr at det er en tilfeldig, ikke-lineære forholdet
mellom de to variablene
Merk at r er en dimensionless kvantitet, dvs. at det ikke er avhengig av enheter
ansatt.
En perfekt korrelasjon på ± 1 oppstår bare når data poeng alle ligge nøyaktig på en
rett linje. Hvis r = +1, skråningen av denne linje som er positivt. Hvis r = -1, skråningen av dette
line er negative.
En sammenheng som er større enn 0.8 er generelt beskrevet som sterk, mens en korrelasjon
mindre enn 0.,5 er generelt beskrevet asweak. Disse verdiene kan variere basert på det
«type» av data som blir undersøkt. En studie utnytte vitenskapelige data kan kreve en sterkere
korrelasjon enn en studie ved hjelp av samfunnsvitenskapelige data.

Den determinasjonskoeffisient, r 2,er nyttig fordi det gir andel av
variansen (variasjonen) for en variabel som er forutsigbar fra den andre variabelen.,
Det er et tiltak som gjør det mulig for oss å finne ut hvor sikker man kan være med å gjøre
spådommer fra en bestemt modell/diagram.
Den determinasjonskoeffisient er forholdet mellom forklart variasjon til den totale
variasjon.
Den determinasjonskoeffisient er slik at 0 < r 2 < 1, og angir styrken
av den lineære sammenhengen mellom x og y.,
Den determinasjonskoeffisient representerer prosent av de data som er nærmest
til den linjen som passer best. For eksempel, hvis r = 0.922, trykk deretter r 2 = 0.850, noe som betyr at
85% av den totale variasjon iny kan forklares ved lineær sammenheng mellom x
og y (som beskrevet av regresjonsligningen). De andre 15% av den totale variasjonen
y er fortsatt uforklart.
Den determinasjonskoeffisient er et mål på hvor godt regresjons-linje
representerer data., Hvis regresjons-linje går nøyaktig gjennom hvert punkt på
scatter-plot, det ville være i stand til å forklare all variasjon. Videre linjen er
borte fra punktene, jo mindre det er i stand til å forklare.