
I denne artikkelen, vil du lære om SVM eller Support Vector Machine, som er en av de mest populære AI algoritmer (det er en av de topp 10 AI algoritmer) og om Kjernen Triks, som omhandler ikke-linearitet og høyere dimensjoner., Vi vil berøre emner som hyperplanes, Lagrange Multiplikatorer, vi vil ha visuelle eksempler og kode eksempler (lik den koden som eksempel brukes i KNN kapittel) for bedre å forstå dette svært viktig algoritme.
SVM Forklart
Support Vector Machine er et overvåket læring algoritme for det meste brukt for klassifisering, men det kan brukes også for regresjon. Den viktigste ideen er at basert på de merkede dataene (treningsdata) algoritmen prøver å finne den optimale hyperplane som kan brukes til å klassifisere nye data poeng. I to dimensjoner hyperplane er en enkel linje.,
Vanligvis et lærings-algoritmen prøver å lære de vanligste kjennetegn (det som skiller en klasse fra en annen) av en klasse, og klassifiseringen er basert på de representative egenskaper lært (slik klassifisering er basert på forskjeller mellom klasser). Den SVM fungerer den andre veien rundt. Det finner de fleste lignende eksempler mellom klasser. De vil være støtte vektorer.
Som et eksempel, kan du vurdere to klasser, epler og sitroner.,
Andre algoritmer vil lære mest tydelig, mest representative egenskaper av epler og sitroner, som epler er grønne og avrundet mens sitroner er gul og har elliptiske form.
I motsetning, SVM vil søke etter epler som er svært lik sitroner, for eksempel epler som er gul og har elliptiske form. Dette vil være en støtte vektor. Den andre support vector vil være en sitron som ligner en apple (grønn og avrundet). Så andre algoritmer lærer forskjellene mens SVM lærer likheter.,
Hvis vi visualiserer eksemplet ovenfor i 2D, vi vil ha noe som dette:

når vi går fra venstre til høyre, alle eksemplene vil bli klassifisert som epler til vi når den gule apple. Fra dette punktet, i tillit til at et nytt eksempel er en apple-dråper mens sitron klasse tillit øker., Når sitron klasse tillit blir større enn apple klasse tillit, nye eksempler vil bli klassifisert som sitroner (et sted mellom gult apple og grønn sitron).
Basert på disse støtte vektorer, algoritmen prøver å finne den beste hyperplane som skiller klassene. I 2D-den hyperplane er en linje, så ville det se ut som dette:

Ok, men hvorfor gjorde jeg trekker den blå grensen, som på bildet over?, Jeg kunne også trekke grenser som dette:

Som du kan se, vi har et uendelig antall muligheter for å trekke vedtaket grensen. Så hvordan kan vi finne den optimale en?
å Finne den Optimale Hyperplane
Intuitivt den beste linjen er den linjen som er langt borte fra både apple og lemon eksempler (har den største margin)., For å ha optimal løsning, vi har for å maksimere margin på begge måter (hvis vi har flere klasser, så har vi for å maksimere den vurderer hver av klassene).

Så hvis vi sammenligner bildet med bildet nedenfor, kan vi lett observere, at den første er den optimale hyperplane (linje) og den andre er en sub-optimal løsning, fordi margin er langt kortere.,

Fordi vi ønsker å maksimere marginer å ta i betraktning alle klasser, i stedet for å bruke en margin for hver klasse, bruker vi en «global» margin, som tar i betraktning alle klasser., Dette margin ville se ut som den lilla linjen i følgende bilde:

Denne marginen er ortogonale til grensen, og like langt til støtte vektorer.
Så der har vi vektorer? Hver av beregningene (beregne avstand og optimal hyperplanes) er laget i vektorstyrt plass, slik at hvert datapunkt er ansett som en vektor. Dimensjonen på plass er definert ved antall attributter av eksempler., For å forstå matematikken bak, kan du lese denne korte matematisk beskrivelse av vektorer, hyperplanes og optimaliseringer: SVM Succintly.
alt i Alt, støtte vektorer er datapunkter som definerer posisjon og margin av hyperplane. Vi kaller dem «støtte» vektorer, fordi disse er de representative data poeng av klasser, hvis vi flytter en av dem, posisjon og/eller marginen vil endre. Flytting av andre data poeng, vil ikke ha effekt over margen eller plasseringen av hyperplane.,
for Å gjøre klassifikasjoner, vi trenger ikke alle treningsdata poeng (som i tilfelle av KNN), vi må bare lagre støtte vektorer. I verste fall alle punktene vil være støtte vektorer, men dette er veldig sjeldent, og hvis det skjer, så bør du sjekke din modell for feil eller bugs.
Så i utgangspunktet læring er ekvivalent med å finne hyperplane med de beste margin, så det er en enkel optimalisering problem.,/h2>
De grunnleggende trinnene i SVM er:
- velg to hyperplanes (i 2D) som skiller data med ingen poeng mellom dem (røde linjer)
- maksimere deres avstand (margin)
- den gjennomsnittlige linje (her linjen halvveis mellom de to røde linjer) vil være vedtaket grensen
Dette er veldig hyggelig og enkelt, men å finne den beste margin, optimalisering problemet er ikke trivielt (det er lett i 2D, når vi bare har to attributter, men hva hvis vi har N dimensjoner med N et veldig stort tall)
for Å løse optimalisering problem, vi bruker Lagrange Multiplikatorer., For å forstå denne teknikken kan du lese følgende to artikler: Dualitet Langrange Multiplikator og En Enkel Forklaring på Hvorfor Langrange Multiplikatorer Wroks.
Til nå har vi hatt lineært separable data, slik at vi kunne bruke en linje som klasse grensen. Men hva hvis vi har til å håndtere ikke-lineær datasett?,
SVM for Ikke-Lineære datasett
Et eksempel på ikke-lineær data er:

I dette tilfellet kan vi ikke finne en rett linje for å skille epler fra sitroner. Så hvordan kan vi løse dette problemet. Vi vil bruke Kernel Lure!
Den grunnleggende ideen er at når et datasett er uatskillelige i gjeldende mål, legge til en annen dimensjon, kanskje på den måten, vil data bli separable., Bare tenk på det, er eksemplet ovenfor er i 2D, og det er uatskillelige, men kanskje i 3D-det er et gap mellom epler og sitroner, kanskje det er et nivå forskjell, så sitroner er på nivå én og sitroner er på nivå to. I dette tilfellet kan vi lett trekke et skille hyperplane (i 3D med et hyperplane er et fly) mellom nivå 1 og 2.
Mapping til Høyere Dimensjoner
for Å løse dette problemet bør vi ikke bare blindt legge til en annen dimensjon, vi bør forandre på plass slik at vi genererer dette nivået forskjell med hensikt.,
Mapping fra 2D til 3D
La oss anta at vi legger til en annen dimensjon kalt X3. En annen viktig transformasjon er at i den nye dimensjonen poeng er organisert ved hjelp av denne formelen x12 + x22.
Hvis vi plotte planet definert av x2 + y2 formel, vil vi få noe som dette:

Nå har vi til kart epler og sitroner (som er like enkle poeng) denne nye plassen. Tenk på det nøye, hva gjorde vi?, Vi brukte bare en transformasjon som vi har lagt til nivåer basert på avstand. Hvis du er i opphavet, så vil det antall poeng vil være på det laveste nivået. Som vi beveger oss bort fra det opprinnelige, det betyr at vi er klatring bakken (flytting fra midten av flyet mot marginer), slik at nivået av punktene vil være høyere., Nå hvis vi mener at opprinnelsen er sitron fra sentrum, vi vil ha noe som dette:
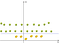
Nå kan vi enkelt skille de to klassene. Disse endringene kalles kjerner. Populære kjerner er: Polynom Kjernen, Gauss-Kjernen, Radial Grunnlag Funksjon (RBF), Laplace RBF-Kjernen, Sigmoid Kjernen, Anove RBF-Kjernen, etc (se Kernel Funksjoner eller en mer detaljert beskrivelse maskinlæring Kjerner).,
Mapping fra 1D til 2D
en Annen, enklere eksempel i 2D vil være:

Etter bruk av kjernen og etter alle endringene som vi vil få:

Så etter transformasjon, vi kan lett avgrense de to klassene ved hjelp av bare en enkelt linje.,
I det virkelige liv programmer vi ikke har en enkel rett linje, men vi vil ha massevis av kurver og høye mål. I noen tilfeller vil vi ikke ha to hyperplanes som skiller data med ingen poeng mellom dem, så vi trenger noen trade-offs, toleranse for uteliggere. Heldigvis SVM-algoritmen har en såkalt regularization parameter for å konfigurere trade-off og til å tolerere uteliggere.
Tuning Parametere
Som vi så i forrige avsnitt velge riktig kjernen er avgjørende, fordi hvis transformasjon er feil, så kan modellen har svært dårlige resultater., Som en tommelfingerregel, alltid sjekk om du har lineær data, og i så fall alltid bruke lineær SVM (lineær kernel). Lineær SVM er en parametrisk modell, men en RBF-kjernen SVM ikke er det, så kompleksiteten av sistnevnte vokser med størrelsen på opplæring sett. Ikke bare er dyrere å trene en RBF-kjernen SVM, men du har også å holde kjerne matrix rundt, og kan settes inn i dette «uendelig» høyere dimensjonale rom der data blir lineært separable er dyrere så godt under prediksjon., Videre, du har mer hyperparameters å stille, så valg av modell er dyrere, så vel! Og til slutt, det er mye lettere å overfit en kompleks modell!
Regularization
Regularization Parameter (i python er det som kalles C) forteller SVM optimalisering hvor mye du vil unngå å gå glipp av å klassifisere hver trening eksempel.
Hvis C er høyere, optimalisering vil velge mindre margin hyperplane, så trening data glipp klassifisering pris vil være lavere.,
På den annen side, hvis C er lave, så marginen vil være store, selv om det vil være savner klassifisert treningsdata eksempler. Dette er vist i de to følgende diagrammer:

Som du kan se i bildet, når C er lav, margin er høyere (slik implisitt vi ikke har så mange svinger, linje ikke strengt følger datapunkter) selv om to epler ble klassifisert som sitroner., Når C er høy, og den grensen er full av kurver og all trening data ble klassifisert riktig. Ikke glem at selv om alle treningsdata ble riktig klassifisert, dette betyr ikke at økt C alltid vil øke presisjonen (på grunn av overfitting).
Gamma
Den neste viktige parameter er Gamma. Gamma parameteren definerer hvor langt påvirkning av en enkelt trening for eksempel når. Dette betyr at høy Gamma vil vurdere eneste poeng nær plausibel hyperplane og lav Gamma vil vurdere poeng på større avstand.,

Som du kan se, redusere Gamma vil føre til at det å finne den riktige hyperplane vil vurdere poeng på større avstander slik at flere og flere poeng vil bli brukt (grønne linjer angir hvilke punkter som ble tatt i betraktning da å finne den optimale hyperplane).
Margin
Den siste parameteren er margin. Vi har allerede snakket om marginer, høyere margin resultatene bedre modell, så bedre klassifisering (eller logisk skriving)., Marginen bør alltid være maksimert.
SVM Eksempel ved hjelp av Python
I dette eksempelet vil vi bruke Social_Networks_Ads.csv-filen, den samme filen som vi brukte i forrige artikkel, se KNN eksempel ved hjelp av Python.
I dette eksempelet vil jeg skrive ned bare forskjeller mellom SVM og KNN, fordi jeg ikke ønsker å gjenta meg selv i hver artikkel! Hvis du vil hele forklaring om hvordan vi kan lese dataene, hvordan kan vi analysere og dele våre data eller hvordan kan vi vurdere eller tomten beslutningen om grenser, så kan du lese koden eksempel fra forrige kapittel (KNN)!,
Fordi sklearn biblioteket er en svært godt skrevet og nyttig Python library, vi har ikke for mye kode for å endre. Den eneste forskjellen er at vi har å importere SVC-klasse (SVC = SVM i sklearn) fra sklearn.svm i stedet for KNeighborsClassifier klasse fra sklearn.nabo.
Etter import av SVC, kan vi lage vår nye modell ved å bruke de forhåndsdefinerte constructor. Dette constructor har mange parametere, men jeg vil bare beskrive de viktigste, mesteparten av tiden vil du ikke bruke andre parametre.,
De viktigste parametrene er:
- kjerne: kjernen type som skal brukes. Den vanligste kjerner er rbf (dette er standard verdi), poly eller sigmoid, men du kan også lage din egen kjerne.,
- C: dette er regularization parameter som er beskrevet i Tuning Parametere seksjonen
- gamma: dette ble også beskrevet i Tuning Parametere seksjonen
- grad: det brukes bare hvis valgt kjernen er poly og angir graden av polinom
- sannsynlighet: dette er en boolsk parameter, og hvis det er sant, da er den modellen kommer tilbake for hver prediksjon, vektor for sannsynligheten for å tilhøre hver klasse av responsvariabel. Så i utgangspunktet vil det gi deg den confidences for hver prediksjon.,
- krympende: dette viser om du ønsker eller ikke ønsker en krympende heuristisk brukt i optimaliseringen av SVM, som er brukt i Sekvensiell Minimal Optimalisering. Det er standard verdi er sant, en hvis du ikke har en god grunn til det, kan du ikke endre denne verdien er false, fordi reduksjonen vil i stor grad forbedre ytelsen, for svært lite tap i form av nøyaktighet i de fleste tilfeller.
Nå kan se resultatet av å kjøre denne koden., Beslutningen om grensen for trening sett ser ut som dette:

Som vi kan se, og som vi har lært i Tuning Parametere delen, fordi C har liten verdi (0.1) beslutningen om grensen er glatt.
hvis vi Nå øke C fra 0.,1 til 100 som vi vil ha flere kurver i vedtaket grensen:

Hva ville skje hvis vi bruker C=0.1 men nå øker vi Gamma fra 0,1 til 10? Lar se!

Hva skjedde her? Hvorfor har vi så dårlig modell?, Som du har sett i Tuning Parametere delen, høy gamma betyr at ved beregning av sannsynlig hyperplane vi ser kun på poeng, som er i nærheten. Nå er fordi tettheten av grønne poeng er høy bare på det valgte grønt område, i den regionen punktene er nær nok til plausibel hyperplane, så de hyperplanes ble valgt. Vær forsiktig med gamma parameter, fordi dette kan ha en svært dårlig innflytelse over resultatene av modellen hvis du setter den til en svært høy verdi (hva er en «svært høy verdi» avhenger av tettheten av data poeng).,
For dette eksemplet er de beste verdiene for C og Gamma er 1.0 og 1.0. Hvis vi nå kjører vår modell på test sett vil vi få følgende diagram:

Og den Forvirring Matrix ser ut som dette:

Som du kan se, vi har bare 3 Falske Positiver, og bare 4 Falske Negativer., Nøyaktigheten av denne modellen er det 93% som er et virkelig godt resultat, vi fikk et bedre resultat enn ved bruk av KNN (som hadde en nøyaktighet på 80%).
MERK: nøyaktighet er ikke den eneste beregningen brukes i ML, og heller ikke den beste beregning for å evaluere en modell, på grunn av Nøyaktigheten Paradoks. Vi bruker denne beregningen, for enkelhet, men senere, i kapittel Beregninger for å Vurdere AI Algoritmer vi vil snakke om Nøyaktigheten Paradoks, og jeg vil vise andre svært populære beregninger brukt i dette feltet.,
Konklusjon
I denne artikkelen har vi sett en meget populære og kraftige overvåket læring algoritme, Support Vector Machine. Vi har lært den grunnleggende ideen, hva er en hyperplane, hva er støtte vektorer og hvorfor er de så viktige. Vi har også sett mange visuelle representasjoner, som hjalp oss å bedre forstå alle begrepene.
et Annet viktig tema som vi rørte er Kjernen Triks, som hjalp oss å løse ikke-lineære problemer.
Å ha en bedre modell, så vi teknikker for å tune algoritmen., På slutten av artikkelen vi hadde en kode eksempel i Python, som viste oss hvordan vi kan bruke KNN-algoritmen.
Som den siste tanker, ønsker jeg å gi noen fordeler & ulemper, og noen populære bruke tilfeller.,
Proffene
– >
- SVN kan være svært effektiv, fordi den bruker bare et delsett av treningsdata, bare støtte vektorer
- Fungerer veldig bra på mindre datasett, på ikke-lineær datasett og høy dimensjonal områder
- Er svært effektiv i tilfeller der antall dimensjoner er større enn antall prøver
- Det kan ha høy nøyaktighet, noen ganger kan utføre enda bedre enn nevrale nettverk
- Ikke veldig følsom for overfitting
Ulemper
– >
- Opplæring tiden er høye når vi har store datasett
- Når datasettet har mer støy (jeg.,e. målet klasser er overlappende) SVM utfører ikke godt
Populære Bruke Tilfeller
– >
- Tekst Klassifisering
- for å Oppdage spam
- Sentiment-analyse
- Aspekt-basert anerkjennelse
- Aspekt-basert anerkjennelse
- Håndskrevne sifret anerkjennelse
