Geometrische sequenties en sommen

sequentie

een sequentie is een verzameling van dingen (meestal getallen) die in orde zijn.

Geometrische sequenties

In een geometrische sequentie wordt elke term gevonden door de vorige term te vermenigvuldigen met een constante.

in het algemeen schrijven we een geometrische reeks als deze:

{a, ar, ar2, ar3, …, }

waarbij:

a de eerste term is, en
r de factor is tussen de termen (de “common ratio”genoemd)

maar wees voorzichtig, r zou niet 0 moeten zijn:

wanneer r=0, krijgen we de Reeks {a,0,0,…} die niet geometrisch is

de regel

We kunnen ook elke term berekenen met behulp van de regel:

xn = ar(n-1)

(we gebruiken “n-1” omdat ar0 voor de eerste term is)

een geometrische reeks kan ook kleinere en kleinere waarden hebben:

voorbeeld:

4, 2, 1, 0.5, 0.25, …,

Deze reeks heeft een factor van 0,5 (de helft) tussen elk getal.

De regel is xn = 4 × (0.5)n-1

waarom “Geometrische” sequentie?,

Omdat het is zoals het vergroten van de dimensies in de meetkunde:

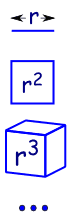	een lijn is 1-dimensionaal en heeft een lengte van r
	in 2 afmetingen van een plein heeft een oppervlakte van r2
	in 3 dimensies een kubus heeft volume r3
	etc (ja we hebben 4 en meer dimensies in de wiskunde).,

Geometrische reeksen worden soms Geometrische progressies (G. P. ‘ S)

som van een geometrische reeks

om deze samen te tellen:

a + ar + ar2 + … + ar(n-1)

(elke term is ark, waar k begint bij 0 en gaat tot n-1)

We kunnen deze handige formule gebruiken:

a is de eerste term
r is de” common ratio ” tussen termen
n is het aantal termen

Wat is dat grappige Σ symbool?, Het heet Sigma notatie

(genaamd Sigma) betekent “Som”

en onder en boven het worden de begin-en eindwaarden getoond:

er staat “som n op waar n van 1 naar 4 gaat. Answer = 10

De formule is eenvoudig te gebruiken …, gewoon “plug in” de waarden van a, r en n

met behulp van de Formule

laten we de formule in Actie bekijken:

voorbeeld: rijstkorrels op een schaakbord

Op de pagina binaire cijfers geven we een voorbeeld van korrels van rijst op een schaakbord. De vraag wordt gesteld:

wanneer we rijst op een schaakbord plaatsen:

1 korrel op het eerste vierkant,
2 korrels op het tweede vierkant,
4 korrels op het derde,
…

… verdubbeling van de rijstkorrels op elk vierkant …

…, hoeveel rijstkorrels in totaal?

we hebben Dus:

a = 1 (de eerste term)
r = 2 (twee per keer)
n = 64 (64 vakjes op een schaakbord)

Dus:

Is:

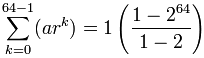
= 1-264-1 = 264 − 1

= 18,446,744,073,709,551,615

en Dat was precies het resultaat dat we kregen op de Binaire Cijfers pagina (god zij dank!)

en een ander voorbeeld, deze keer met r minder dan 1:

Waarom werkt de Formule?,

laten we eens kijken waarom de formule werkt, omdat we een interessante “truc” kunnen gebruiken die de moeite waard is om te weten.

noem eerst de hele som “S”: S = A + ar + ar2 + … + ar(n−2) + ar(n−1)

vervolgens vermenigvuldigt u s met r:S·r = ar + ar2 + ar3+… + ar(n−1) + arn

merk op dat S en S·r vergelijkbaar zijn?

trek ze nu af!

Wow! Alle termen in het midden heffen netjes op.,
(wat een nette truc is)

door S·r van S af te trekken krijgen we een eenvoudig resultaat:

S − S·r = a − arn

laten we het herschikken om s te vinden:

Factor out s en a:S(1−r) = a(1−rn)

delen door (1−r):S = A(1−RN)(1−R)

wat onze formule is (ta-da!):

oneindige geometrische reeks

dus wat gebeurt er als n oneindig wordt?,

We kunnen deze formule gebruiken:

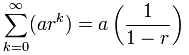
maar wees voorzichtig:

r moet tussen (maar niet inclusief) -1 en 1

en r moet niet 0 zijn omdat de Reeks {a,0,0,…} is niet geometrisch

dus onze infnite Geometrische serie heeft een eindige Som wanneer de verhouding kleiner is dan 1 (en groter dan -1)

laten we ons vorige voorbeeld terugnemen en zien wat er gebeurt:

geloof me niet? Kijk gewoon naar dit vierkant:

door optellen 12 + 14 + 18 + …

we eindigen met het hele ding!,

terugkerende decimaal

op een andere pagina vroegen we “doet 0,999… gelijk aan 1?”, nou, laten we eens kijken of we het kunnen berekenen: