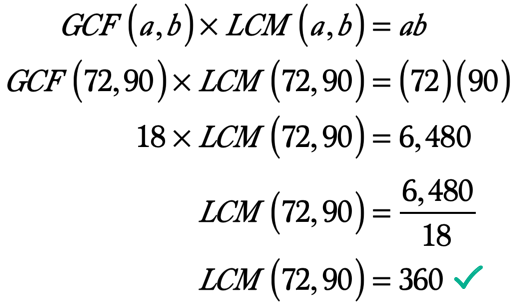toen u bestudeerde hoe u de GCF en LCM van twee positieve getallen kon vinden, ontdekte u toen een zeer interessante relatie tussen de twee grootheden?

Ik deed! Ik ontdekte het per ongeluk toen ik een jonge student was en ik dacht dat ik iets vond dat “revolutionair”was. Ik was zo opgewonden dat ik het deelde met mijn leraar., Maar tot mijn frustratie keek hij me aan en zei dat het al een bewezen wiskundige uitspraak was. Ik voelde me even ontmoedigd, maar ik ging terug naar mijn schoolwerk en ging verder.

Als u het nog niet bent tegengekomen, is er een opmerkelijke algebraïsche relatie of link tussen de grootste gemeenschappelijke Factor (GCF) en de kleinste gemeenschappelijke veelvoud (LCM) van twee getallen. In deze les zijn de getallen die we willen alleen die behoren tot de verzameling van positieve gehele getallen.,
Hieronder is de algebraïsche verbinding tussen de GCF en de LCM van twee positieve gehele getallen.
de Formule GCF-LCM
waarschuwing: de Formule”GCF-LCM” bestaat echt niet. Ik verzon de naam voor het gemak van verwijzing. Je mag het noemen wat je wilt, zolang het zijn doel dient.,
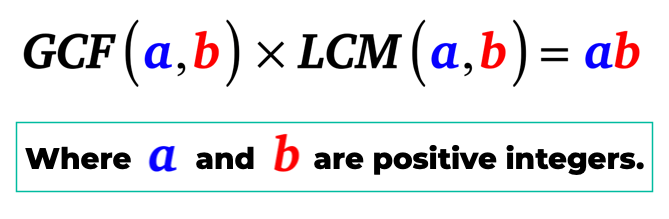
factor A en B wanneer vermenigvuldigd tot het kleinste gemene veelvoud van A en B is gelijk aan het product van A en B. dat wil zeggen, A en B zijn positieve gehele getallen.
voorbeeldproblemen
Voorbeeld 1: de GCF van 12 en 16 is 4. Wat is de LCM van 12 en 16?
u kunt de LCM van 12 en 16 bepalen met behulp van een van de twee onderstaande methoden.,
- LCM vinden met behulp van de Lijstmethode
- LCM vinden met behulp van de Priemelfactorisatiemethode
Er is echter een veel snellere manier. U kunt gebruik maken van de” GCF-LCM formule ” omdat u de twee gehele getallen en zijn GCF kent. Steek gewoon de waarden in de formule en los vervolgens op voor de LCM.
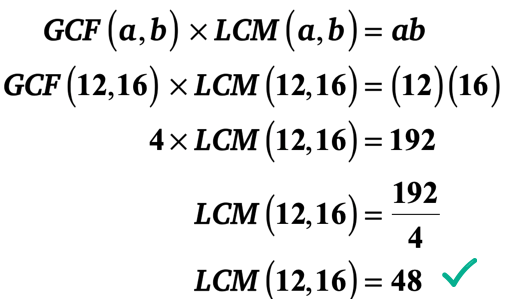
Ik laat het aan u over om te controleren of de LCM van 12 en 16 inderdaad 48 is.
Voorbeeld 2: de LCM van 24 en 40 is 120. Wat is de GCF van 24 en 40?,
dit probleem is precies het tegenovergestelde van Voorbeeld 1 omdat je de waarde van de LCM krijgt in plaats van GCF.
dus dit is de informatie die we kennen. Laten we ze specificeren voor de duidelijkheid.
l LCM (24,40) = 120
▶ ︎ a=24 en B=40 daarom ab = \left( {24} \right)\left( {40} \right) = 960
note opmerking: het maakt niet echt uit welke getallen A en B zijn. het zal de uitkomst van het uiteindelijke antwoord niet veranderen. Het is echter een goede praktijk om uw oplossing te standaardiseren. Ik stel voor dat je A het kleinere geheel getal laat zijn terwijl b het grotere geheel getal is.,
laten we de bekende waarden in de formule vervangen en dan oplossen voor de GCF van 24 en 40.
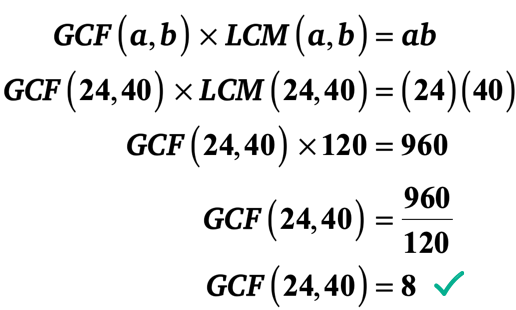
Voorbeeld 3: Zoek de GCF van 20 en 25 door eerst de LCM van 20 en 25 te berekenen.
dit probleem zal enigszins verschillen van de voorbeelden #1 en #2. Je moet eerst de kleinste gemene veelvoud (LCM) van 20 en 25 berekenen. Daarna kunt u oplossen voor de grootste gemeenschappelijke Factor (GCF) van 20 en 25 met behulp van de GCF-LCM formule.
dus hier gaan we!, Om de LCM van 20 en 25 te vinden, zullen we de eerste paar veelvouden van 20 en 25 schrijven. De allereerste gemeenschappelijke veelvoud die verschijnt zal onze LCM zijn.
veelvouden van 20: 20, 40, 60, 80, 100, 120
veelvouden van 25: 25, 50, 75, 100, 125, 150
aangezien het getal 100 verschijnt als het eerste veelvoud van 20 en 25, kunnen we claimen dat de LCM van 20 en 25 100 is.
we hebben nu alle informatie om de formule te gebruiken. Hieronder staan de waarden die we gaan vervangen in de formule op te lossen voor de LCM van 20 en 25.,
◉ Het product van a en b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ De LCM van 20 en 25 → LCM\left( {20,25} \right) = 100
Hier is de berekening op te lossen voor de GCF van 20 en 25:
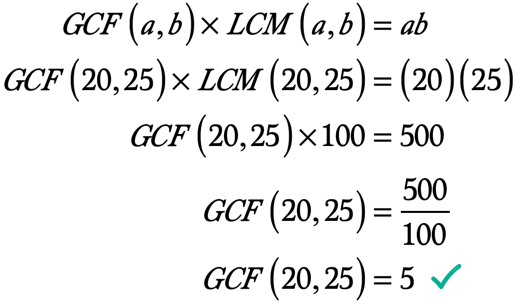
Voorbeeld 4: het Vinden van de LCM van 63 en 84 door eerst de berekening van de GCF van 63 en 84.
dit probleem lijkt erg op Voorbeeld #3. Het enige verschil is dat je eerst de GCF berekent in plaats van de LCM, zoals geïnstrueerd door het probleem zelf.,
laten we alle factoren van 63 en 84 vinden. Je kunt de “rainbow method” techniek gebruiken om de gegeven gehele getallen te factor.
merk op dat de grootste Of hoogste gemeenschappelijke factor tussen de twee lijsten 21 is.
factoren van 63: 1, 3, 7, 9, 21, 63
factoren van 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
daarom is de grootste gemeenschappelijke Factor van 63 en 84 21. Dus GCF \ left ({63,84} \ right) = 21.,
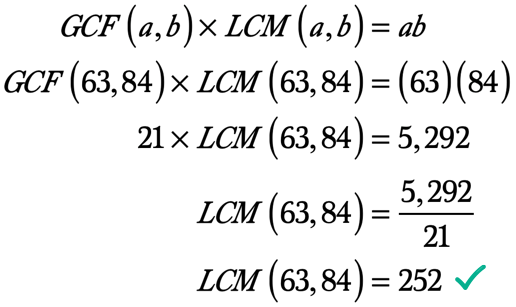
Voorbeeld 5: Zoek de LCM van 72 en 90 met behulp van de Formule GCF-LCM.
zoals we al weten, kunnen we de LCM van twee gehele getallen met de waarde van zijn GCF vinden met behulp van de GCF-LCM formule.,
een opsomming van zowel de factoren 72 en 90, hebben we:
alle factoren van 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
alle factoren van 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
als we de lijsten van factoren vergelijken, zien we dat 18 de factor is die voor beide hetzelfde is, maar de grootste Of grootste waarde heeft. Het betekent dat de GCF van 72 en 90 18 is, dat wil zeggen, GCF \ left ({72,90} \ right) = 18.
We zijn nu klaar om de onderstaande waarden in de formule te vervangen.,
ab ab = \ left ({72} \right)\left ({90} \right) = 6,480
❖ GCF\left ({72,90} \right) = 18
Hier is de berekening om de LCM te vinden gegeven dat we al de GCF van de twee gehele getallen en hun product kennen.