De makkelijkste manier om het idee van een groeiende populatie te vangen is met een eencellig organisme, zoals een bacterie of een cilliaat. In Figuur 1 wordt een populatie van Paramecium in een kleine laboratoriumdepressiedia afgebeeld. In deze populatie delen de individuen één keer per dag. Dus, beginnend met een enkel individu op dag 0, verwachten we, in opeenvolgende dagen, 2, 4, 8, 16, 32, en 64 individuen in de bevolking., We kunnen hier zien dat, op een bepaalde dag, het aantal individuen in de populatie gewoon twee keer zo groot is als het aantal de dag ervoor, dus het aantal vandaag, noem het N(vandaag), is gelijk aan twee keer het aantal gisteren, noem het N(gisteren), wat we compacter kunnen schrijven als N(vandaag) = 2N(gisteren).
dus is het zinvol om dit te schrijven als, N ( t) = 2N(t – 1) Waar t elke waarde zou kunnen aannemen.,
nu kunnen we dit idee een beetje veralgemenen als we merken dat op dag zes het getal gelijk is aan tweemaal het getal op dag vijf, of N(6) = 2N(5) en op dag vijf het getal gelijk is aan tweemaal het getal op dag vier, of N(5) = 2N(4), enz.
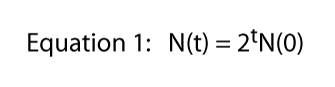
waarbij t staat voor een willekeurig tijdstip (bijvoorbeeld als t = 6, N(6) = 26).
ten slotte merken we op dat deze vergelijking werd afgeleid van de specifieke situatie in Figuur 1, waar één deling per dag de harde en snelle regel was., Dat is waar de 2 vandaan komt in vergelijking 1-van elk individueel Paramecium krijgen we de volgende dag twee individuen. Natuurlijk kan de verdeling van alles zijn. Als er twee divisies per dag waren, maar één cel stierf altijd, zouden we drie individuen verwachten van elk afzonderlijk individu en vergelijking 1 zou N(t) = 3tN(0) zijn., Dus de delingssnelheid kan gelijk welk getal zijn en de algemene vergelijking wordt,
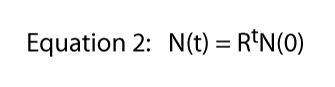
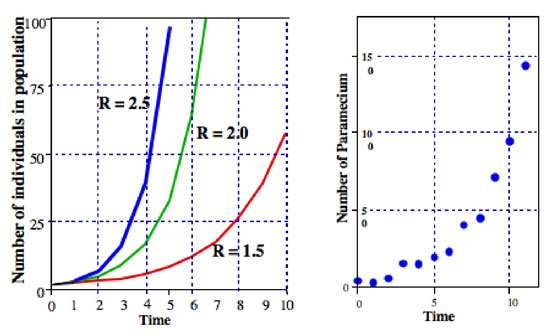
waar R gewoonlijk de eindige snelheid van populatiestijging wordt genoemd (in het werkelijke geval van het delen van Paramecium de eindige snelheid van populatiestijging is gelijk aan de delingspercentage). In Figuur 2 illustreren we deze vergelijking voor verschillende waarden van R. Het wordt normaal gesproken aangeduid als de exponentiële vergelijking, en de vorm van de gegevens in Figuur 2 is de algemene vorm genaamd exponentieel.,
elke waarde van R kan op een oneindig aantal manieren worden weergegeven (bijvoorbeeld, als R = 16, kunnen we r = 8 x 2 schrijven, of R = 42, of R = 32/2, of R = 2.718282.77). Die laatste uitdrukking (R = 2.718282.,77) maakt gebruik van een belangrijke constante die uit de elementaire calculus, de constante van Euler, zou kunnen worden teruggeroepen. Het uitdrukken van de waarde van R als Euler ‘ s constante verhoogd tot een bepaalde macht is eigenlijk uiterst nuttig-het brengt de volledige kracht van de calculus in beeld.,olize Euler ‘ s constante e kunnen we schrijven de Vergelijking 2 als
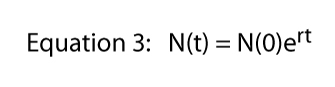
als we de natuurlijke logaritme van beide kanten van de Vergelijking 3 onthouden ln(ex) = x — Vergelijking 3 wordt: ln = ln + rt
En als we begonnen met de bevolking van een enkel individu (zoals in het voorbeeld hierboven), we hebben

uit, waarin we zien dat de natuurlijke logaritme van de bevolking, op een bepaalde tijd, is de enige constante, de tijden die tijd., De constante r wordt aangeduid als de intrinsieke snelheid van natuurlijke toename (Figuur 2).
alle soorten micro-organismen vertonen patronen die zeer dicht bij de exponentiële Bevolkingsgroei liggen. Bijvoorbeeld, in de rechter grafiek van Figuur 2 is een populatie van Paramecium die in een laboratoriumcultuur groeit. Het groeipatroon is zeer dicht bij het patroon van de exponentiële vergelijking.
een andere manier om de exponentiële vergelijking te schrijven is als een differentiaalvergelijking, dat wil zeggen, die de groei van de populatie in zijn dynamische vorm weergeeft., In plaats van de vraag wat is de omvang van de populatie op tijdstip t is, vragen we, wat is de snelheid waarmee de bevolking groeit op tijdstip t. Het tarief wordt gesymboliseerd als dN/dt wat simpelweg betekent “wijzigen in N ten opzichte van de wijziging in t,” en als u oproepen van uw basis-calculus, kunnen we de snelheid van de groei door het differentiëren van Vergelijking 4, dat geeft ons
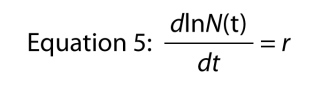
wat is eigenlijk opmerkelijk, want het zegt dat de snelheid van de groei van de log van het aantal in de populatie constant is., Die constante groeisnelheid van de log van de bevolking is de intrinsieke groeisnelheid.,
Herinneren dat de snelheid van verandering van het logaritme van een getal is hetzelfde als het “per capita” verandering in die aantal, dat betekent dat we kunnen schrijven Vergelijking 5

waar we het weglaten van de variabele t, aangezien het duidelijk is waar het over gaat, en dan hebben we herschikken een beetje te komen met
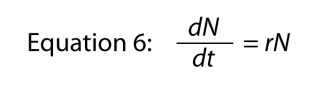
waar de parameter r is, nogmaals, de intrinsieke snelheid van de natuurlijke verhogen., De basisrelatie tussen de eindige verhogingssnelheid en de intrinsieke snelheid is
r = ln(R)
waarbij ln verwijst naar de natuurlijke logaritme. Merk op dat Vergelijking 6 en vergelijking 3 gewoon verschillende vormen van dezelfde vergelijking zijn (Vergelijking 3 is de geïntegreerde vorm van vergelijking 6; vergelijking 6 is de gedifferentieerde vorm van vergelijking 3), en beide kunnen eenvoudig worden aangeduid als de exponentiële vergelijking.,

de exponentiële vergelijking is een nuttig model van eenvoudige populaties, ten minste voor relatief korte perioden., Bijvoorbeeld, als een laboratorium technicus moet weten wanneer een bacteriecultuur een bepaalde bevolkingsdichtheid bereikt, kan de exponentiële vergelijking worden gebruikt om een voorspelling te verstrekken over precies wanneer die populatiegrootte zal worden bereikt. Een ander voorbeeld is het geval van ongedierte in de landbouw. Herbivoren zijn altijd potentieel grote problemen voor planten. Wanneer de aan dergelijke uitbraken blootgestelde planten landbouwgewassen zijn, dat wil zeggen gewassen, kan het verlies zowel voor de landbouwer als voor de consument zeer groot zijn. Er is dus altijd druk om dergelijke uitbraken te voorkomen., Sinds de Tweede Wereldoorlog is het belangrijkste wapen in de bestrijding van dergelijke pest uitbraken chemische bestrijdingsmiddelen, zoals DDT. De laatste jaren zijn wij ons echter gaan realiseren dat deze pesticiden op lange termijn uiterst gevaarlijk zijn, zowel voor het milieu als voor de mens. Bijgevolg is er een beweging geweest om de hoeveelheid pesticiden die worden gespoten om ongedierte te bestrijden te beperken. De belangrijkste manier waarop dit wordt gedaan is om een economische drempel vast te stellen, dat is de bevolkingsdichtheid van de potentiële plaag waaronder de schade aan het gewas onbeduidend is (dat wil zeggen, het is niet echt nodig om te spuiten)., Wanneer de pestpopulatie boven die drempel stijgt, moet de Boer actie ondernemen en een soort pesticide of andere middelen toepassen om de plaag te bestrijden. Gezien de aard van dit probleem is het soms van het grootste belang om te kunnen voorspellen wanneer de plaag de economische drempel zal bereiken. Het kennen van de R voor de plaagsoort stelt de landbouwer in staat te voorspellen wanneer het nodig zal zijn een soort controleprocedure toe te passen (Figuur 3).
de exponentiële vergelijking is ook een nuttig model voor het ontwikkelen van intuïtieve ideeën over populaties., Het klassieke voorbeeld is een vijver met een populatie leliepads. Als elke leliepad zich reproduceert (twee pads nemen de plaats in van waar een pad was geweest) elke maand, en het duurde, laten we zeggen, drie jaar voor de vijver om half gevuld met leliepads te worden, hoeveel langer zal het duren voor de vijver volledig bedekt met leliepads? Als je niet stopt om te helder na te denken, is het verleidelijk om te zeggen dat het net zo veel tijd, drie jaar, zal duren voordat de tweede helft van de vijver zo gevuld is als de eerste. Het antwoord is natuurlijk een maand., een ander populair voorbeeld is de spreekwoordelijke oud-Egyptische (of soms Perzische) wiskundige die betaling van de koning vraagt in de vorm van graankorrels (soms rijst). Een korrel op het eerste vierkant van een schaakbord, twee korrel op het tweede vierkant, enzovoort, tot het laatste vierkant. De farao kan zich niet voorstellen dat zo ‘ n eenvoudige betaling veel zou kunnen betekenen, en gaat daarmee akkoord. Maar hij waardeerde exponentiële groei niet ten volle., Aangezien er 64 vierkanten op het schaakbord staan, kunnen we vergelijking 2 gebruiken om te bepalen hoeveel graankorrels op het laatste vierkant moeten betalen (R verhoogd tot de 64e macht, wat ongeveer 18,446,744,074,000,000,000 is — veel tarwe inderdaad, zeker meer dan in het hele Koninkrijk). Deze voorbeelden benadrukken de vaak verrassende manier waarop een exponentieel proces zeer snel tot zeer grote aantallen kan leiden.
