Snel Antwoord:
Voor een rechthoekige driehoek:

De functie sinus zonde duurt hoek θ en geeft de verhouding tegenover de schuine zijde
De inverse van de sinus functie sin-1 de verhouding oppositehypotenuse en geeft de hoek θ
En cosinus en tangens volgen een vergelijkbaar idee.,
en nu voor de details:
sinus, cosinus en tangens zijn allemaal gebaseerd op een rechthoekige driehoek
ze zijn zeer vergelijkbare functies … dus we zullen kijken naar de sinusfunctie en dan Inverse sinus om te leren waar het allemaal over gaat.,
sinusfunctie
de sinus van hoek θ is:
- De lengte van de zijde tegenover hoek θ
- gedeeld door de lengte van de hypotenusa
of eenvoudiger:
sin(θ) = tegenover / hypotenusa
de sinusfunctie kan ons helpen dit soort dingen op te lossen:
inverse sinusfunctie
maar soms is het de hoek die we moeten vinden.
Hier komt” Inverse sinus ” voor.
het beantwoordt de vraag ” welke hoek heeft sinus gelijk aan tegenovergestelde / hypotenusa?,”
Het symbool voor inverse sinus is sin-1, of soms arcsin.
ze zijn als vooruit en achteruit!

- sin neemt een hoek en geeft ons de verhouding”tegenover/hypotenusa “
- sin-1 neemt de verhouding” tegenover/hypotenusa ” en geeft ons de hoek.
voorbeeld:
| op de rekenmachine drukt u op een van de volgende (afhankelijk van uw merk rekenmachine): “2ndF sin” of “shift sin”. |
op uw rekenmachine, probeer sin en dan sin-1 te gebruiken om te zien wat er gebeurt
meer dan één hoek!
Inverse sinus toont u slechts één hoek … maar er zijn meer hoeken die kunnen werken.
voorbeeld: hier zijn twee hoeken waarbij tegenovergesteld / hypotenusa = 0.,5
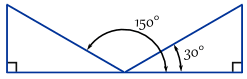
In feite zijn er oneindig veel hoeken, omdat je 360°kunt blijven optellen (of aftrekken):
onthoud dit, want er zijn tijden dat je een van de andere hoeken nodig hebt!
Summary
de sinus van hoek θ is:
sin(θ) = tegenover / hypotenusa
en Inverse sinus is :
sin-1 (tegenover / hypotenusa) = θ
hoe zit het met “cos” en “tan” … ?
precies hetzelfde idee, maar verschillende zijverhoudingen.,
Hoek
De Cosinus van de hoek θ is:
cos(θ) = Grenzend / schuine zijde
En de Inverse Cosinus is :
cos-1 (Naast / schuine zijde) = θ
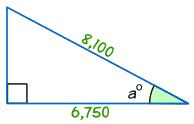
Voorbeeld: de grootte van hoek a°
cos a° = Grenzend / schuine zijde
cos a° = 6,750/8,100 = 0.8333…
a° = cos-1 (0,8333…) = 33.,6° (op 1 decimaal)
de Raaklijn
De Tangens van de hoek θ is:
tan(θ) = het Tegenovergestelde / Aangrenzende
Dus de Inverse Tangens :
tan-1 (Tegenover / Naast) = θ
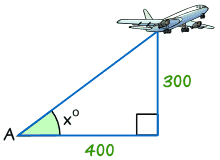
Voorbeeld: De grootte van de hoek x°
tan x° = het Tegenovergestelde / Aangrenzende
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (correct tot op 1 decimaal)
andere namen
soms wordt sin-1 asin of arcsin
genoemd en ook cos-1 wordt acos of arccos
genoemd en tan-1 wordt atan of arctan
voorbeelden:
- arcsin(y) is hetzelfde als sin-1(y)
- atan(θ) is hetzelfde als tan-1(θ)
- enz.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- maar de Inverse sinus en inverse cosinus “gaan niet eeuwig door” zoals sinus en cosinus doen …
laten we eens kijken naar het voorbeeld van cosinus.
Hier is de cosinus en de Inverse cosinus uitgezet op dezelfde grafiek:
cosinus en de inverse cosinus
het zijn spiegelbeelden (over de diagonaal)
maar waarom wordt de inverse cosinus aan de boven-en onderkant afgehakt (de puntjes maken niet echt deel uit van de functie) … ?
omdat het een functie is, kan het slechts één antwoord geven
als we vragen “Wat is cos-1 (x)?,”
één antwoord of oneindig veel antwoorden
maar we zagen eerder dat er oneindig veel antwoorden zijn, en de stippellijn op de grafiek toont dit.
dus ja er zijn oneindig veel antwoorden …
… maar stel je voor dat je 0.5 intypt in je rekenmachine, druk op cos-1 en het geeft je een nooit eindigende lijst van mogelijke antwoorden …
dus we hebben deze regel dat een functie slechts één antwoord kan geven.
dus, door het zo af te hakken krijgen we maar één antwoord, maar we moeten niet vergeten dat er andere antwoorden kunnen zijn.,
raaklijn en Inverse raaklijn
en hier is de raaklijnfunctie en inverse raaklijn. Kun je zien hoe ze zijn spiegelbeelden (over de diagonaal) …?

Tangent

Inverse Tangent




