Na het bouwen van een machine learning model, de volgende stap is het evalueren van het model van de prestaties en begrijpen hoe goed is ons model tegen een benchmark model., De te gebruiken evaluatie-maatstaf hangt af van het type probleem dat u probeert op te lossen —of het een probleem is onder toezicht of zonder toezicht, en of het een classificatie of een regressietaak is.
In dit artikel ga ik het hebben over twee belangrijke evaluatie metrics gebruikt voor regressieproblemen en de nadruk leggen op het belangrijkste verschil tussen hen.
R-kwadraat, ook bekend als de coëfficiënt bepaling, bepaalt de mate waarin de variantie in de afhankelijke variabele (of doel) kan worden verklaard door de onafhankelijke variabele (kenmerken).,
laten we dit begrijpen met een voorbeeld — stel dat de R-kwadraatwaarde voor een bepaald model 0,7 is. Dit betekent dat 70% van de variatie in de afhankelijke variabele wordt verklaard door de onafhankelijke variabelen.
idealiter zouden we willen dat de onafhankelijke variabelen in staat zijn om alle variatie in de doelvariabele te verklaren. In dat scenario zou de R-kwadraatwaarde 1 zijn. Dus kunnen we zeggen dat hoger de R-kwadraat waarde, beter in het model.,
dus, in eenvoudige termen, hoger de R kwadraat, de meer variatie wordt verklaard door uw input variabelen en dus beter is uw model. Ook zou de R-kwadraat variëren van 0 tot 1. Hier is de formule voor het berekenen van R-kwadraat –
Het R-kwadraat wordt berekend door de som van de kwadraten van reststoffen uit het regressiemodel (gegeven door SSRE ‘ s) te delen door de totale som van de kwadraten van fouten uit het gemiddelde model (gegeven door SStot) en deze vervolgens af te trekken van 1.,
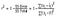
Eén nadeel van r-kwadraat is dat het veronderstelt dat elke variabele helpt bij het verklaren van de variatie in het doel, wat misschien niet altijd waar is. Bijvoorbeeld, als we een nieuwe functies toevoegen aan de gegevens (die al dan niet nuttig kunnen zijn), zou de R-kwadraat waarde voor het model ofwel toenemen of hetzelfde blijven, maar het zou nooit afnemen.
Dit wordt geregeld door een enigszins gewijzigde versie van r-kwadraat, De aangepaste R-kwadraat genaamd.,
aangepast R-kwadraat
vergelijkbaar met R-kwadraat meet de aangepaste R-kwadraat de variatie in de afhankelijke variabele (of target), alleen verklaard door de kenmerken die nuttig zijn bij het maken van voorspellingen. In tegenstelling tot R-kwadraat, zou de aangepaste R-kwadraat je straffen voor het toevoegen van functies die niet nuttig zijn voor het voorspellen van het doel.
laat ons wiskundig begrijpen hoe deze functie is ondergebracht in Aangepast R-kwadraat., Hier is de formule voor aangepast R-kwadraat

Hier is r^2 het berekende R-kwadraat, n het aantal rijen en M het aantal kolommen. Naarmate het aantal functies toeneemt, neemt de waarde in de noemer af.
- als de R2 met een significante waarde toeneemt, dan zou het gecorrigeerde R-kwadraat toenemen.
- indien er geen significante verandering in R2 optreedt, zou de gecorrigeerde r2 afnemen.
