de hoeveelheid r, de zogenaamde lineaire correlatiecoëfficiënt, meet de sterkte en
de richting van een lineaire relatie tussen twee variabelen. De lineaire correlatie
coëfficiënt wordt soms aangeduid als de Pearson product moment correlation coefficient in
eer van de ontwikkelaar Karl Pearson.
de wiskundige formule voor berekening R is: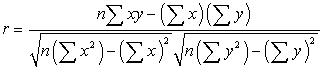

waarbij n het aantal gegevensparen is.,
(Ben je niet blij dat je een grafische rekenmachine hebt die deze formule berekent?)
de waarde van r is zodanig dat -1 < r < +1. De + en – tekens worden gebruikt voor respectievelijk positieve
lineaire correlaties en negatieve lineaire correlaties.
positieve correlatie: als x en y een sterke positieve lineaire correlatie hebben,is r dichtbij
+1. Een r-waarde van exact +1 geeft een perfecte positieve pasvorm aan., Positieve waarden
wijzen op een relatie tussen X-en y-variabelen, zodat wanneer de waarden voor x toenemen,
– waarden voor y ook toenemen.
negatieve correlatie: als x en y een sterke negatieve lineaire correlatie hebben,is r dichtbij
tot -1. Een r-waarde van Exact -1 geeft een perfecte negatieve pasvorm aan. Negatieve waarden
geven een relatie aan tussen x en y, zodat als waarden voor x stijgen, waarden
Voor y afnemen.
geen correlatie: als er geen lineaire correlatie of een zwakke lineaire correlatie is, is r
dicht bij 0., Een waarde in de buurt van nul betekent dat er een willekeurige, niet-lineaire relatie
tussen de twee variabelen
merk op dat r een dimensieloze hoeveelheid is; dat wil zeggen, het is niet afhankelijk van de gebruikte eenheden
.
een perfecte correlatie van ± 1 treedt alleen op wanneer de gegevenspunten allemaal precies op een
rechte lijn liggen. Als r = + 1, is de helling van deze lijn positief. Als r = -1, is de helling van deze
lijn negatief.
een correlatie groter dan 0,8 wordt over het algemeen als sterk beschreven, terwijl een correlatie
kleiner dan 0.,5 wordt over het algemeen beschreven als weak. Deze waarden kunnen variëren op basis van het
“Type” van de gegevens die worden onderzocht. Voor een studie waarin wetenschappelijke gegevens worden gebruikt, kan een sterkere correlatie nodig zijn dan voor een studie waarin sociaalwetenschappelijke gegevens worden gebruikt.

de determinatiecoëfficiënt, r 2,is nuttig omdat het de verhouding van
de variantie (fluctuatie) van een variabele geeft die voorspelbaar is van de andere variabele.,
Het is een maat die ons in staat stelt om te bepalen hoe zeker men kan zijn in het maken van
voorspellingen uit een bepaald model/grafiek.
de determinatiecoëfficiënt is de verhouding tussen de verklaarde variatie en de totale
variatie.
de determinatiecoëfficiënt is zodanig dat 0 < r 2 < 1, en geeft de sterkte
van de lineaire associatie tussen x en y aan.,
de determinatiecoëfficiënt vertegenwoordigt het percentage van de gegevens dat
het dichtst bij de regel van de beste pasvorm ligt. Bijvoorbeeld, als r = 0,922, dan r 2 = 0,850, wat betekent dat
85% van de totale variatie iny kan worden verklaard door de lineaire relatie tussen x
en y (zoals beschreven door de regressievergelijking). De overige 15% van de totale variatie
In y blijft onverklaard.
de determinatiecoëfficiënt is een maat voor de mate waarin de regressielijn
de gegevens weergeeft., Als de regressielijn precies door elk punt van het
scatterplot gaat, kan deze alle variatie verklaren. Hoe verder de lijn
van de punten verwijderd is, hoe minder hij kan verklaren.