SVM en Kernel SVM

In dit artikel leer je meer over SVM of Support Vector Machine, dat is een van de meest populaire AI-algoritmen (het is een van de top 10 AI-algoritmen) en over de Kernel Trick, die zich bezighoudt met de niet-lineariteit en hogere dimensies., We zullen onderwerpen als hyperplanes, Lagrange Multipliers, we zullen visuele voorbeelden en code voorbeelden (vergelijkbaar met de code voorbeeld gebruikt in het KNN hoofdstuk) om dit zeer belangrijke algoritme beter te begrijpen.

SVM uitgelegd

De Support Vector Machine is een begeleid leren algoritme meestal gebruikt voor classificatie, maar het kan ook worden gebruikt voor regressie. Het belangrijkste idee is dat op basis van de gelabelde data (trainingsdata) het algoritme probeert het optimale hypervlak te vinden dat kan worden gebruikt om nieuwe datapunten te classificeren. In twee dimensies is het hypervlak een eenvoudige lijn.,

gewoonlijk probeert een leeralgoritme de meest voorkomende kenmerken (wat een klasse van een andere onderscheidt) van een klasse te leren en de classificatie is gebaseerd op die representatieve geleerde kenmerken (dus classificatie is gebaseerd op verschillen tussen klassen). De SVM werkt andersom. Het vindt de meest vergelijkbare voorbeelden tussen de klassen. Dat zijn de dragers.

als voorbeeld, laten we twee klassen beschouwen, appels en citroenen.,

andere algoritmen zullen de meest evidente, meest representatieve kenmerken van appels en citroenen leren, zoals appels groen en afgerond zijn, terwijl citroenen geel zijn en elliptische vorm hebben.

daarentegen zal SVM zoeken naar appels die sterk lijken op citroenen, bijvoorbeeld appels die geel zijn en elliptische vorm hebben. Dit zal een ondersteuningsvector zijn. De andere steun vector zal een citroen vergelijkbaar met een appel (groen en afgerond). Dus andere algoritmen leert de verschillen, terwijl SVM leert overeenkomsten.,

Als we visualiseren het bovenstaande voorbeeld in 2D zal zijn, hebben wij iets als dit:

Als we gaan van links naar rechts, alle voorbeelden worden geclassificeerd als appels tot we bij de gele appel. Vanaf dit punt daalt het vertrouwen dat een nieuw voorbeeld een appel is, terwijl het vertrouwen van de citroenklasse toeneemt., Wanneer het vertrouwen van de citroenklasse groter wordt dan het vertrouwen van de appelklasse, worden de nieuwe voorbeelden geclassificeerd als citroenen (ergens tussen de gele appel en de groene citroen).

Op basis van deze ondersteuningsvectoren probeert het algoritme het beste hypervlak te vinden dat de klassen scheidt. In 2D de hyperplane is een lijn, dus het zou er als volgt uitzien:

Ok, maar waarom deed ik teken de blauwe grens, zoals in de foto hierboven?, Ik zou ook grenzen als deze kunnen tekenen:

zoals u kunt zien, hebben we een oneindig aantal mogelijkheden om de beslissingsgrens te tekenen. Dus hoe kunnen we de optimale vinden?

het optimale hypervlak vinden

intuïtief is de beste lijn de lijn die ver weg is van zowel appel-als citroenvoorbeelden (heeft de grootste marge)., Om een optimale oplossing te hebben, moeten we de marge op beide manieren maximaliseren (als we meerdere klassen hebben, dan moeten we deze maximaliseren gezien elk van de klassen).

dus als we de afbeelding hierboven vergelijken met de afbeelding hieronder, kunnen we gemakkelijk zien, dat de eerste het optimale hypervlak (lijn) is en de tweede een suboptimale oplossing is, omdat de marge veel korter is.,

omdat we de marges willen maximaliseren rekening houdend met alle klassen, gebruiken we in plaats van één marge voor elke klasse, een “globale” marge, die alle klassen in aanmerking neemt., Deze marge zou lijken op de paarse lijn in de volgende afbeelding:

Deze marge is loodrecht op de grens en op gelijke afstand tot de support vectoren.

dus waar hebben we vectoren? Elk van de berekeningen (bereken afstand en optimale hypervlakken) worden gemaakt in vectoriële ruimte, zodat elk gegevenspunt wordt beschouwd als een vector. De dimensie van de ruimte wordt bepaald door het aantal attributen van de voorbeelden., Om de wiskunde erachter te begrijpen, lees dan deze korte wiskundige beschrijving van vectoren, hyperplanes en optimalisaties: SVM beknopt.

al met al zijn ondersteuningsvectoren gegevenspunten die de positie en de marge van het hypervlak bepalen. We noemen ze “support” vectoren, omdat dit de representatieve datapunten van de klassen zijn, als we een van hen verplaatsen, zal de positie en/of de marge veranderen. Het verplaatsen van andere datapunten zal geen effect hebben over de marge of de positie van het hypervlak.,

om classificaties te maken, hebben we niet alle trainingsgegevenspunten nodig (zoals in het geval van KNN), we hoeven alleen de ondersteuningsvectoren op te slaan. In het ergste geval zullen alle punten ondersteuning vectoren zijn, maar dit is zeer zeldzaam en als het gebeurt, dan moet je je model controleren op fouten of bugs.

dus in principe is het leren equivalent met het vinden van het hypervlak met de beste marge, dus het is een eenvoudig optimalisatieprobleem.,/h2>

De basis stappen van de SVM zijn:

1. kies twee hyperplanes (in 2D) die het scheidt de gegevens zonder punten tussen hen (rode lijnen)
2. het maximaliseren van hun afstand (de marge)
3. de gemiddelde lijn (hier de lijn halverwege tussen de twee rode lijnen) zal de beslissing grens

Dit is erg leuk en makkelijk, maar het vinden van de beste marge, de optimalisatie probleem is niet triviaal (het is gemakkelijk in 2D, als we slechts twee attributen, maar wat als we N dimensies, met N een groot getal)

Aan het oplossen van de optimalisatie probleem, we maken gebruik van de Lagrange Multiplicatoren., Om deze techniek te begrijpen kunt u de volgende twee artikelen lezen: dualiteit Langrange Multiplier en een eenvoudige uitleg van waarom Langrange Multipliers Wroks.

tot nu toe hadden we lineair scheidbare data, dus we konden een lijn gebruiken als klasse grens. Maar wat als we te maken hebben met niet-lineaire datasets?,

SVM voor niet-lineaire datasets

een voorbeeld van niet-lineaire gegevens is:

in dit geval kunnen we geen rechte lijn vinden om appels van citroenen te scheiden. Dus hoe kunnen we dit probleem oplossen. We zullen de Kerneltruc gebruiken!

het basisidee is dat wanneer een gegevensset onafscheidelijk is in de huidige dimensies, een andere dimensie toevoegt, misschien op die manier zullen de gegevens scheidbaar zijn., Denk er eens over na, het voorbeeld hierboven is in 2D en het is onafscheidelijk, maar misschien is er in 3D een kloof tussen de appels en de citroenen, misschien is er een niveauverschil, dus citroenen zijn op niveau één en citroenen zijn op niveau twee. In dit geval kunnen we gemakkelijk een scheidend hypervlak tekenen (in 3D is een hypervlak een vlak) tussen niveau 1 en 2.

Mapping naar hogere dimensies

om dit probleem op te lossen moeten we niet blindelings een andere dimensie toevoegen, we moeten de ruimte transformeren zodat we dit niveauverschil opzettelijk genereren.,

Mapping van 2D naar 3D

laten we aannemen dat we een andere dimensie toevoegen genaamd X3. Een andere belangrijke transformatie is dat in de nieuwe dimensie de punten worden georganiseerd met behulp van deze formule x12 + x22.

als we het door de X2 + y2 formule gedefinieerde vlak plotten, krijgen we zoiets als dit:

nu moeten we de appels en citroenen (die slechts eenvoudige punten zijn) in kaart brengen naar deze nieuwe ruimte. Denk er goed over na, wat hebben we gedaan?, We gebruikten net een transformatie waarbij we niveaus optelden op basis van afstand. Als je in de oorsprong, dan zullen de punten op het laagste niveau. Als we ons van de oorsprong verwijderen, betekent dit dat we de heuvel beklimmen (vanuit het midden van het vlak naar de marges bewegen) zodat het niveau van de punten hoger zal zijn., Als wij nu overwegen, dat de oorsprong is van de citroen van het centrum, we zullen iets als dit:

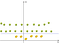
Nu kunnen we gemakkelijk scheiden van de twee klassen. Deze transformaties worden kernels genoemd. Populaire kernels zijn: polynomiale Kernel, Gaussiaanse Kernel, radiale basisfunctie (RBF), Laplace RBF Kernel, Sigmoid Kernel, Anove RBF Kernel, etc. (Zie Kernel functies of een meer gedetailleerde beschrijving Machine Learning Kernels).,

Mapping van 1D 2D

een Andere, eenvoudiger voorbeeld in 2D zou zijn:

Na het gebruik van de kernel en nadat alle voor de transformaties krijgen we:

Dus na de transformatie, we kunnen gemakkelijk scheiden van de twee klassen met behulp van slechts een enkele lijn.,

in real life toepassingen zullen we geen eenvoudige rechte lijn hebben, maar we zullen veel krommen en hoge dimensies hebben. In sommige gevallen zullen we geen twee hypervliegtuigen hebben die de gegevens scheiden zonder punten ertussen, dus hebben we wat afwegingen nodig, tolerantie voor uitschieters. Gelukkig heeft het SVM-algoritme een zogenaamde regularisatieparameter om de trade-off te configureren en uitschieters te tolereren.

Tuning Parameters

zoals we in de vorige paragraaf zagen is het kiezen van de juiste kernel cruciaal, want als de transformatie onjuist is, dan kan het model zeer slechte resultaten hebben., Als vuistregel moet je altijd controleren of je lineaire data hebt en in dat geval altijd lineaire SVM (lineaire kernel) gebruiken. Lineaire SVM is een parametrisch model, maar een RBF kernel SVM niet, dus de complexiteit van de laatste groeit met de grootte van de trainingsset. Niet alleen is het duurder om een RBF kernel SVM te trainen, maar je moet ook de kernelmatrix rondhouden, en de projectie in deze” oneindige ” hogere dimensionale ruimte waar de gegevens lineair scheidbaar worden is ook duurder tijdens de voorspelling., Bovendien heb je meer hyperparameters om af te stemmen, dus modelselectie is ook duurder! En tot slot is het veel gemakkelijker om een complex model over te steken!

regularisatie

De Regularisatieparameter (in python heet het C) vertelt de SVM-optimalisatie hoe graag u wilt voorkomen dat u het classificeren van elk trainingsvoorbeeld mist.

als de C hoger is, zal de optimalisatie kleinere marge hyperplane kiezen, zodat de training data miss classification rate lager zal zijn.,

aan de andere kant, als de C laag is, dan zal de marge groot zijn, zelfs als er mis geclassificeerde opleidingsgegevens voorbeelden zullen zijn. Dit wordt weergegeven in de volgende twee diagrammen:

zoals je in de afbeelding kunt zien, is de marge hoger als de C laag is (dus impliciet hebben we niet zoveel krommen, de lijn volgt niet strikt de datapunten) zelfs als twee appels geclassificeerd werden als citroenen., Wanneer de C hoog is, is de grens vol bochten en zijn alle trainingsgegevens correct geclassificeerd. Vergeet niet, zelfs als alle trainingsgegevens correct waren geclassificeerd, betekent dit niet dat het verhogen van de C altijd de precisie zal verhogen (door overbevissing).

Gamma

De volgende belangrijke parameter is Gamma. De gammaparameter bepaalt hoe ver de invloed van een enkel trainingsvoorbeeld reikt. Dit betekent dat hoge Gamma alleen punten in aanmerking neemt die dicht bij het plausibele hypervlak liggen en lage Gamma alleen punten op grotere afstand.,

Zoals je kan zien, het verminderen van de Gamma zal resulteren dat het vinden van de juiste hyperplane zal overwegen punten op grotere afstanden dus meer en meer punten zal worden gebruikt (groene lijnen aangegeven welke punten zijn overwogen bij het vinden van de optimale hyperplane).

marge

de laatste parameter is de marge. We hebben al gesproken over marge, hogere marge resultaten beter model, dus betere classificatie (of voorspelling)., De marge moet altijd worden gemaximaliseerd.

SVM voorbeeld Python gebruiken

In dit voorbeeld zullen we de Social_Networks_Ads gebruiken.csv bestand, hetzelfde bestand als in het vorige artikel, zie KNN voorbeeld Python gebruiken.

in dit voorbeeld zal ik alleen de verschillen tussen SVM en KNN opschrijven, omdat ik mezelf niet in elk artikel wil herhalen! Als u de hele uitleg wilt over hoe we de dataset kunnen lezen, hoe we onze gegevens kunnen ontleden en splitsen of hoe we de beslissingsgrenzen kunnen evalueren of plotten, lees dan het codevoorbeeld uit het vorige hoofdstuk (KNN)!,

omdat de sklearn bibliotheek een zeer goed geschreven en nuttige Python bibliotheek is, hebben we niet te veel code om te veranderen. Het enige verschil is dat we de SVC klasse (SVC = SVM in sklearn) moeten importeren vanuit sklearn.svm in plaats van de KNeighborsClassifier klasse van sklearn.buurman.

na het importeren van de SVC, kunnen we ons nieuwe model maken met behulp van de vooraf gedefinieerde constructor. Deze constructor heeft veel parameters, maar Ik zal alleen de belangrijkste beschrijven, meestal gebruik je geen andere parameters.,

de belangrijkste parameters zijn:

1. kernel: het kerneltype dat moet worden gebruikt. De meest voorkomende kernels zijn rbf (dit is de standaard waarde), poly of sigmoid, maar je kunt ook je eigen kernel aanmaken.,
2. C: Dit is de regularisatieparameter beschreven in de Tuning Parameters sectie
3. gamma: dit werd ook beschreven in de Tuning Parameters sectie
4. graad: het wordt alleen gebruikt als de gekozen kernel poly is en de graad van de polinom
5. waarschijnlijkheid instelt: dit is een Booleaanse parameter en als het waar is, dan zal het model voor elke voorspelling de vector van de waarschijnlijkheid van behoren tot elke klasse van de respons variabele teruggeven. Dus in principe geeft het je de vertrouwen voor elke voorspelling.,
6. shrinking: dit geeft aan of u een shrinking heuristic wilt gebruiken in uw optimalisatie van de SVM, die wordt gebruikt in sequentiële minimale optimalisatie. De standaardwaarde is true, en als u geen goede reden hebt, verander deze waarde dan niet in false, omdat krimpen uw prestaties aanzienlijk zal verbeteren, voor zeer weinig verlies in termen van nauwkeurigheid in de meeste gevallen.

laten we nu de uitvoer van het uitvoeren van deze code zien., De beslissingsgrens voor de trainingsset ziet er als volgt uit:

zoals we kunnen zien en zoals we hebben geleerd in de tuning parameters sectie, omdat de C een kleine waarde heeft (0.1) is de beslissingsgrens glad.

als we nu de C van 0 verhogen.,1 tot 100 we zullen meer curves hebben in de beslissingsgrens:

wat zou er gebeuren als we C=0.1 gebruiken, maar nu verhogen we gamma van 0.1 naar 10? Eens kijken!

Wat is hier gebeurd? Waarom hebben we zo ‘ n slecht model?, Zoals je hebt gezien in de Tuning Parameters sectie, hoge gamma betekent dat bij het berekenen van het plausibele hypervlak we alleen punten die dichtbij zijn beschouwen. Omdat de dichtheid van de groene punten alleen in het geselecteerde groene gebied hoog is, liggen de punten in dat gebied dicht genoeg bij het plausibele hypervlak, dus werden die hypervlakken gekozen. Wees voorzichtig met de parameter gamma, want dit kan een zeer slechte invloed hebben op de resultaten van je model als je het op een zeer hoge waarde stelt (wat een “zeer hoge waarde” is, hangt af van de dichtheid van de datapunten).,

in dit voorbeeld zijn de beste waarden voor C en Gamma 1.0 EN 1.0. Nu als wij ons model op de test set krijgen we het volgende schema:

En de Verwarring Matrix ziet er zo uit:

Zoals je kan zien, wij hebben slechts 3 Valse Positieven en op slechts 4 Valse Negatieven., De nauwkeurigheid van dit model is 93% wat een echt goed resultaat is, we hebben een betere score behaald dan met behulp van KNN (die een nauwkeurigheid van 80% had).

opmerking: nauwkeurigheid is niet de enige metriek die in ML wordt gebruikt en ook niet de beste metriek om een model te evalueren, vanwege de Nauwkeurigheidsparadox. We gebruiken deze metriek voor eenvoud, maar later, in het hoofdstuk Metrics om AI-algoritmen te evalueren, zullen we het hebben over de Nauwkeurigheidsparadox en zal ik andere zeer populaire metrics laten zien die op dit gebied worden gebruikt.,

conclusies

in dit artikel hebben we een zeer populair en krachtig begeleid leeralgoritme gezien, de Support Vector Machine. We hebben het basisidee geleerd, wat een hypervlak is, wat ondersteuningsvectoren zijn en waarom ze zo belangrijk zijn. We hebben ook veel visuele representaties gezien, die ons hielpen om alle concepten beter te begrijpen.

een ander belangrijk onderwerp dat we hebben aangeraakt is de Kerneltruc, die ons hielp om niet-lineaire problemen op te lossen.

om een beter model te hebben, zagen we technieken om het algoritme af te stemmen., Aan het einde van het artikel hadden we een code voorbeeld in Python, die ons liet zien hoe we het KNN algoritme kunnen gebruiken.

als laatste gedachten wil ik enkele voors & cons en enkele populaire use cases geven.,

Pluspunten

1. SVN kan heel efficiënt zijn, omdat het gebruik maakt van slechts een deel van de training data, alleen de support vectoren
2. Werkt erg goed op kleinere gegevenssets, op niet-lineaire data sets en hoge dimensionale ruimten
3. zeer effectief zijn in gevallen waar het aantal dimensies is groter dan het aantal monsters
4. Het kan een hoge nauwkeurigheid soms kan het beter dan neurale netwerken
5. Niet erg gevoelig voor overfitting

Nadelen

1. Training is hoog wanneer we grote data sets
2. Wanneer de data set heeft meer lawaai (ik.,e. doelklassen overlappen elkaar) SVM presteert niet goed

populaire Use Cases

1. Tekstclassificatie
2. spam detecteren
3. Sentiment analyse
4. Aspect-based recognition
5. Aspect-based recognition
6. handgeschreven digit recognition