Nach dem Erstellen eines Modells für maschinelles Lernen besteht der nächste Schritt darin, die Modellleistung zu bewerten und zu verstehen, wie gut unser Modell gegen ein Benchmark-Modell ist., Die zu verwendende Bewertungsmetrik hängt von der Art des Problems ab, das Sie lösen möchten —ob es sich um ein überwachtes oder unbeaufsichtigtes Problem handelt und ob es sich um eine Klassifizierungs-oder eine Regressionsaufgabe handelt.
In diesem Beitrag werde ich über zwei wichtige Bewertungsmetriken sprechen, die für Regressionsprobleme verwendet werden, und den Hauptunterschied zwischen ihnen hervorheben.
R-Quadrat, auch als Koeffizientenbestimmung bezeichnet, definiert den Grad, in dem die Varianz in der abhängigen Variablen (oder dem Ziel) durch die unabhängige Variable (Merkmale) erklärt werden kann.,
Lassen Sie uns dies anhand eines Beispiels verstehen — sagen wir, der R-Quadrat-Wert für ein bestimmtes Modell beträgt 0,7. Dies bedeutet, dass 70% der Variation der abhängigen Variablen durch die unabhängigen Variablen erklärt werden.
Idealerweise möchten wir, dass die unabhängigen Variablen alle Variationen in der Zielvariablen erklären können. In diesem Szenario wäre der R-Quadrat-Wert 1. So können wir sagen, dass höher der R-Quadrat-Wert, besser im Modell.,
Also, in einfachen Worten, je höher das R-Quadrat, desto mehr Variation wird durch Ihre Eingabevariablen erklärt und daher ist Ihr Modell besser. Außerdem würde das R-Quadrat von 0 bis 1 reichen. Hier ist die Formel zur Berechnung von R-Quadrat –
Das R-Quadrat wird berechnet, indem die Summe der Quadrate der Residuen aus dem Regressionsmodell (gegeben durch SSres) durch die Gesamtsumme der Fehlerquadrate aus dem Durchschnittsmodell (gegeben durch SStot) dividiert und dann von 1 subtrahiert wird.,
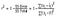
Ein Nachteil von r-squared ist, dass davon ausgegangen wird, dass jede Variable bei der Erklärung der Variation im Ziel hilft, was könnte nicht immer wahr sein. Wenn wir beispielsweise den Daten neue Funktionen hinzufügen (was möglicherweise nützlich ist oder nicht), würde der r-Quadrat-Wert für das Modell entweder zunehmen oder gleich bleiben, aber niemals abnehmen.
Dafür sorgt eine leicht modifizierte Version von r-squared, genannt adjusted r-squared.,
Adjusted R-squared
Ähnlich wie R-squared misst das Adjusted R-squared die Variation der abhängigen Variablen (oder des Ziels), die nur durch die Funktionen erklärt wird, die hilfreich sind, um Vorhersagen zu treffen. Im Gegensatz zu R-Squared würde das angepasste R-Squared Sie dafür bestrafen, Funktionen hinzuzufügen, die für die Vorhersage des Ziels nicht nützlich sind.
Lassen Sie uns mathematisch verstehen, wie diese Funktion im angepassten R-Quadrat untergebracht ist., Hier ist die Formel für das r-Quadrat

Hier ist R^2 das r-Quadrat berechnet, N ist die Anzahl der Zeilen und M ist die Anzahl der Spalten. Mit zunehmender Anzahl von Merkmalen nimmt der Wert im Nenner ab.
- Wenn der R2 um einen signifikanten Wert ansteigt, würde das angepasste r-Quadrat zunehmen.
- Wenn sich R2 nicht signifikant ändert, würde das angepasste r2 abnehmen.
