Statistik 2-Korrelationskoeffizient und Bestimmungskoeffizient

Korrelationskoeffizient

Wie gut repräsentiert Ihre Regressionsgleichung wirklich
Ihren Datensatz?
Eine Möglichkeit, die Antwort auf diese Frage zu bestimmen, besteht darin, den Korrelationskoeffizienten und den Bestimmungskoeffizienten zu untersuchen.,

Die als linearer Korrelationskoeffizient bezeichnete Menge r misst die Stärke und
die Richtung einer linearen Beziehung zwischen zwei Variablen. Der lineare Korrelationskoeffizient
wird in
zu Ehren seines Entwicklers Karl Pearson manchmal als Pearson product moment correlation coefficient bezeichnet.
Die mathematische Formel für die berechnungr ist: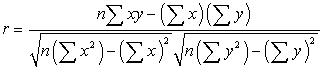

wobei n die Anzahl der Datenpaare ist.,
(Sind Sie nicht froh, dass Sie einen Grafikrechner haben, der diese Formel berechnet?)
Der Wert von r ist, so dass -1 < r < +1. Die + und-Zeichen werden für positive
lineare Korrelationen bzw. negative lineare Korrelationen verwendet.
Positive Korrelation: Wenn x und y eine starke positive lineare Korrelation haben,ist r nahe
an +1. Ein r-Wert von genau +1 zeigt eine perfekte positive Anpassung an., Positive Werte
geben eine Beziehung zwischen x-und y-Variablen an, sodass mit zunehmenden Werten für x auch
– Werte für y zunehmen.
Negative Korrelation: Wenn x und y eine starke negative lineare Korrelation haben,ist r nahe
bei -1. Ein r-Wert von genau -1 zeigt eine perfekte negative Anpassung an. Negative Werte
geben eine Beziehung zwischen x und y an, sodass Werte
für y abnehmen, wenn Werte für x zunehmen.
Keine Korrelation: Wenn es keine lineare Korrelation oder eine schwache lineare Korrelation gibt, ist r
nahe 0., Ein Wert nahe Null bedeutet, dass zwischen den beiden Variablen
eine zufällige, nichtlineare Beziehung

Beachten Sie, dass r eine dimensionslose Größe ist.
Eine perfekte Korrelation von ± 1 tritt nur dann auf, wenn die Datenpunkte alle exakt auf einer
Geraden liegen. Wenn r = +1 ist, ist die Steigung dieser Linie positiv. Wenn r = -1, ist die Steigung dieser
– Linie negativ.
Eine Korrelation größer als 0,8 wird allgemein als stark beschrieben, während eine Korrelation
kleiner als 0 ist.,5 wird allgemein als schwach beschrieben. Diese Werte können je nach dem
„Typ“ der zu untersuchenden Daten variieren. Eine Studie, die wissenschaftliche Daten verwendet, erfordert möglicherweise eine stärkere
– Korrelation als eine Studie, die sozialwissenschaftliche Daten verwendet.

Der Bestimmungskoeffizient, r 2,ist nützlich, da er den Anteil von
der Varianz (Fluktuation) einer Variablen angibt, die von der anderen Variablen vorhersehbar ist.,
Es ist ein Maß, mit dem wir bestimmen können, wie sicher man sein kann, wenn man
Vorhersagen aus einem bestimmten Modell/Diagramm macht.
Der Bestimmungskoeffizient ist das Verhältnis der erklärten Variation zur gesamten
– Variation.
Der Bestimmungskoeffizient ist so, dass 0 < r 2 < 1 und bezeichnet die Stärke
der linearen Assoziation zwischen x und y.,
Der Bestimmungskoeffizient repräsentiert den Prozentsatz der Daten, der der Linie der besten Passform am nächsten kommt
. Wenn zum Beispiel r = 0,922 ist, dann ist r 2 = 0,850, was bedeutet, dass
85% der gesamten Variation iny durch die lineare Beziehung zwischen x
und y erklärt werden können (wie durch die Regressionsgleichung beschrieben). Die anderen 15% der Gesamtvariation
in y bleiben ungeklärt.
Der Bestimmungskoeffizient ist ein Maß dafür, wie gut die Regressionslinie
die Daten darstellt., Wenn die Regressionslinie genau durch jeden Punkt im
– Streudiagramm verläuft, kann sie alle Variationen erklären. Je weiter die Linie von den Punkten entfernt ist, desto weniger kann sie erklären.