Geometriska sekvenser och summor

sekvens

en sekvens är en uppsättning saker (vanligtvis siffror) som är i ordning.

geometriska sekvenser

i en geometrisk sekvens hittas varje term genom att multiplicera föregående term med en konstant.

i allmänhet skriver vi en geometrisk sekvens så här:

{a, ar, ar2, ar3, …, }

var:

a är den första termen, och
r är faktorn mellan termerna (kallas ”common ratio”)

men var försiktig, r bör inte vara 0:

När r=0 får vi sekvensen {a, 0,0,…} som inte är geometrisk

regeln

Vi kan också beräkna vilken term som helst med regeln:

xn = ar(n-1)

(vi använder ”N-1” eftersom ar0 är för 1: A termen)

en geometrisk sekvens kan också ha mindre och mindre värden:

exempel:

4, 2, 1, 0.5, 0.25, …,

denna sekvens har en faktor på 0,5 (en halv) mellan varje nummer.

dess regel är xn = 4 × (0.5)n-1

varför ”geometrisk” sekvens?,

eftersom det är som att öka dimensionerna i geometri:

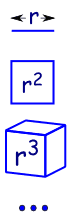	en linje är 1-dimensionell och har en längd på r
	I 2 dimensioner har en kvadrat en yta på R2
	I 3 dimensioner har en kub volym R3
	etc (Ja Vi kan ha 4 och fler dimensioner i matematik).,

geometriska sekvenser kallas ibland Geometriska progressioner (G. P.)

summera en geometrisk serie

för att sammanfatta dessa:

a + ar + ar2 + … + ar(n-1)

(varje term är ark, där k börjar vid 0 och går upp till n-1)

Vi kan använda denna praktiska formel:

a är den första termen
r är det ”gemensamma förhållandet” mellan termer
n är antalet termer

vad är det roliga Σ symbol?, Det kallas Sigma Notation

(kallas Sigma) betyder ”summera”

och under och över det visas start-och slutvärden:

det står ”summera n där n går från 1 till 4. Answer=10

formeln är enkel att använda …, bara ”koppla in” värdena för A, r och n

med formeln

låt oss se formeln i åtgärd:

exempel: riskorn på ett schackbräde

På sidan binära siffror ger vi ett exempel på riskorn på ett schackbräde. Frågan ställs:

När vi placerar ris på ett schackbräde:

1 korn på första torget,
2 korn på andra torget,
4 korn på tredje och så vidare,
…

… fördubbla riskornen på varje kvadrat …

…, hur många korn av ris totalt?

så vi har:

a = 1 (den första termen)
r = 2 (dubblar varje gång)
n = 64 (64 rutor på ett schackbräde)

Så:

blir:

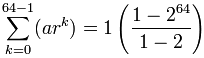
= 1-264-1 = 264 − 1

= 18,446,744,073,709,551,615

vilket var exakt det resultat vi fick på den binära siffror sidan (tack och lov!)

och ett annat exempel, den här gången med r mindre än 1:

Varför fungerar formeln?,

låt oss se varför formeln fungerar, eftersom vi får använda ett intressant ”trick” som är värt att veta.

ring först hela summan ”s”: s = a + ar + ar2 + … + ar(n−2)+ ar (n−1)

nästa, multiplicera s med r:s·r = ar + ar2 + ar3 + … + ar (n−1) + arn

Observera att s och S·r är likartade?

nu subtrahera dem!

Wow! Alla villkor i mitten avbryter snyggt ut.,
(vilket är ett snyggt trick)

genom att subtrahera s·r från S får vi ett enkelt resultat:

s − s·r = a − arn

Låt oss omorganisera det för att hitta s:

faktor ut s och a:S(1−r) = a(1−rn)

dividera med (1−r):s = a(1−rn)(1−r)

vilket är vår formel (ta-da!):

oändlig Geometrisk serie

Så vad händer när n går till oändligheten?,

vi kan använda denna formel:

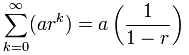
men var försiktig:

r måste vara mellan (men inte inklusive) -1 och 1

och r bör inte vara 0 eftersom sekvensen {a,0,0,…} är inte geometrisk

så vår infnite geometriska serie har en ändlig summa när förhållandet är mindre än 1 (och större än -1)

Låt oss ta tillbaka vårt tidigare exempel och se vad som händer:

tro mig inte? Titta bara på denna ruta:

genom att lägga till 12 + 14 + 18 + .- herr talman!..

vi slutar med det hela!,

återkommande Decimal

på en annan sida frågade vi ”Does 0.999… lika 1?”, låt oss se om vi kan beräkna det: