det enklaste sättet att fånga tanken på en växande befolkning är med en enda cellad organism, såsom en bakterie eller en cilliat. I Figur 1, en population av Paramecium i ett litet laboratorium depression bild. I denna population delar individerna en gång per dag. Så, från och med en enda individ på dag 0, förväntar vi oss, i successiva dagar, 2, 4, 8, 16, 32, och 64 personer i befolkningen., Vi kan se här att, på en viss dag, antalet individer i befolkningen är helt enkelt dubbelt så många som antalet var dagen innan, så numret idag, kalla det N (idag), är lika med dubbelt så många igår, kalla det N(igår), som vi kan skriva mer kompakt som N(idag) = 2N(igår).
så det är vettigt att skriva detta som, N(t) = 2N(t – 1) där t kunde ta på något värde alls.,
Nu kan vi generalisera denna idé lite om vi noterar att på dag sex är numret lika med dubbelt så många som på dag fem, eller N(6) = 2N(5) och på dag fem är numret lika med dubbelt så många på dag fyra, eller n(5) = 2N(4) etc.
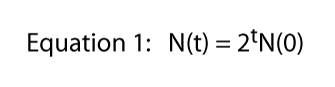
var t står för när som helst (t.ex. om T = 6, n(6) = 26).
slutligen noterar vi att denna ekvation härleddes från den specifika situationen som visas i Figur 1, där en division per dag var den hårda och snabba regeln., Det är där 2 kommer från i ekvation 1 — från varje enskild Paramecium får vi två individer nästa dag. Naturligtvis kan divisionen vara vad som helst. Om det fanns två divisioner per dag men en cell dog alltid, skulle vi förvänta oss tre individer från varje enskild individ och ekvation 1 skulle vara N (t) = 3tN(0)., Så divisionshastigheten kan vara vilket nummer som helst och den allmänna ekvationen blir,
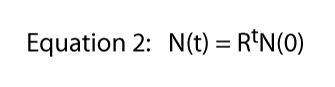
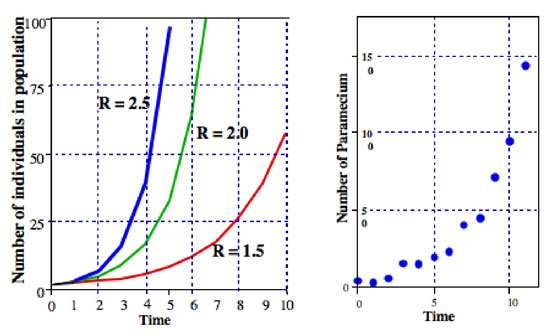
Där R vanligtvis kallas den ändliga befolkningsökningen (i det faktiska fallet med delningsparamecium är den ändliga befolkningsökningen lika med divisionshastigheten). I Figur 2 illustrerar vi denna ekvation för olika värden av R. det kallas normalt exponentiell ekvation, och formen av data i Figur 2 är den allmänna formen kallad exponentiell.,
alla värden på R kan representeras på ett oändligt antal sätt (t.ex. om R = 16, kan vi skriva R = 8 x 2, eller r = 42, eller R = 32/2, eller R = 2.718282.77). Det sista uttrycket (R = 2.718282.,77) använder sig av en viktig konstant som kan återkallas från elementär kalkyl, Euler konstant. Att uttrycka vilket värde som helst av R som Eulers konstanta höjda till viss kraft är faktiskt extremt användbar – det ger full kraft av kalkyl i bilden.,olize Eulers konstant som e vi kan skriva ekvation 2 som
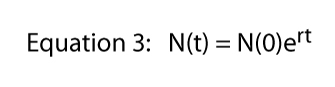
Nu om vi tar den naturliga loggen på båda sidor av ekvation 3 — kom ihåg ln(ex) = X — ekvation 3 blir: ln = LN + rt
och om vi började befolkningen med en enda individ (som i exemplet ovan) har vi

från vilken vi ser att befolkningens naturliga logg, vid vilken tidpunkt som helst, är någon konstant, gånger den tiden., Konstant r kallas den naturliga ökningstakten (Figur 2).
alla typer av mikroorganismer uppvisar mönster som ligger mycket nära exponentiell befolkningstillväxt. Till exempel, i högra grafen i Figur 2 är en population av Paramecium som växer i en laboratoriekultur. Mönstret av tillväxt ligger mycket nära mönstret för den exponentiella ekvationen.
ett annat sätt att skriva exponentiell ekvation är som en differentialekvation, det vill säga representerar befolkningens tillväxt i sin dynamiska form., Snarare än att fråga vad som är storleken på befolkningen vid tiden t frågar vi, vad är den takt som befolkningen växer vid tiden t. hastigheten symboliseras som dN/dt vilket helt enkelt betyder ”förändring i n i förhållande till förändring i t” och om du kommer ihåg din grundläggande kalkyl kan vi hitta tillväxttakten genom att differentiera ekvation 4, vilket ger oss
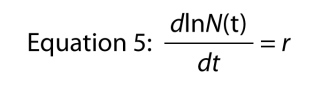
vilket är ganska anmärkningsvärt, eftersom det säger att tillväxten av loggen av antalet i befolkningen är konstant., Den konstanta tillväxttakten i befolkningens logg är den inneboende ökningstakten.,
Kom ihåg att förändringshastigheten för loggen för ett tal är densamma som ”per capita” – förändringen i det numret, vilket innebär att vi kan skriva ekvation 5 som

där vi utelämnar variabeln t eftersom det är uppenbart där det är uppenbart att det är en kommer upp med
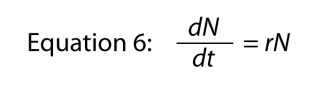
där parametern R är, återigen, den inneboende graden av naturlig ökning., Det grundläggande förhållandet mellan ändlig ökningstakt och inneboende hastighet är
r = ln(R)
där ln refererar till den naturliga logaritmen. Observera att ekvation 6 och ekvation 3 är bara olika former av samma ekvation (ekvation 3 är den integrerade formen av ekvation 6; ekvation 6 är den differentierade formen av ekvation 3), och båda kan kallas helt enkelt som exponentiell ekvation.,

den exponentiella ekvationen är en användbar modell av enkla populationer, åtminstone under relativt korta tidsperioder., Till exempel, om en laboratorietekniker behöver veta när en bakteriekultur når en viss befolkningstäthet, kan exponentiell ekvation användas för att ge en förutsägelse om exakt när den befolkningsstorleken kommer att nås. Ett annat exempel är när det gäller jordbruksskadegörare. Växtätare är alltid potentiellt stora problem för växter. När de växter som utsätts för sådana utbrott är jordbruk, det vill säga grödor, kan förlusten vara mycket betydelsefull för både jordbrukare och konsumenter. Således finns det alltid tryck för att förhindra sådana utbrott., Sedan andra världskriget det stora vapnet i kampen mot sådana skadedjur utbrott har varit kemiska bekämpningsmedel, såsom DDT. Men under de senaste åren har vi kommit att inse att dessa bekämpningsmedel är extremt farliga på lång sikt, både för miljön och för människor. Följaktligen har det skett en rörelse för att begränsa mängden bekämpningsmedel som sprutas för att bekämpa skadedjur. Det viktigaste sättet att göra detta är att fastställa ett ekonomiskt tröskelvärde, vilket är befolkningstätheten hos det potentiella skadedjuret under vilket skadorna på grödan är obetydliga (dvs det är inte riktigt nödvändigt att spruta)., När pestpopulationen ökar över denna tröskel måste jordbrukaren vidta åtgärder och tillämpa någon form av bekämpningsmedel eller andra medel för att kontrollera skadedjuret. Med tanke på problemets natur är det ibland av yttersta vikt att kunna förutsäga när skadedjuret kommer att nå det ekonomiska tröskelvärdet. Att känna till R för skadedjursarterna gör det möjligt för jordbrukaren att förutsäga när det kommer att bli nödvändigt att tillämpa något slags kontrollförfarande (Figur 3).
exponentiell ekvation är också en användbar modell för att utveckla intuitiva idéer om populationer., Det klassiska exemplet är en damm med en befolkning av liljkuddar. Om varje lilja pad reproducerar sig själv (två kuddar tar platsen där en pad hade varit) varje månad, och det tog, säg, tre år för dammen att bli halv fylld med lilja kuddar, hur mycket längre kommer det att ta för dammen att vara helt täckt med lilja kuddar? Om du inte slutar tänka alltför tydligt, det är frestande att säga att det kommer att ta lika mycket tid, tre år, för den andra halvan av dammen att bli så fylld som den första. Svaret är naturligtvis en månad.,
ett annat populärt exempel är den ökända forntida egyptiska (eller ibland persiska) matematiker som frågar betalning från kungen i form av korn av vete (ibland ris). Ett korn på den första kvadraten av ett schackbräde, två korn på den andra kvadraten, och så vidare, till den sista kvadraten. Farao kan inte föreställa sig att en sådan enkel betalning kan uppgå till mycket, och så håller med. Men han uppskattade inte helt exponentiell tillväxt., Eftersom det finns 64 rutor på schackbrädet kan vi använda ekvation 2 för att bestämma hur många korn av vete som kommer att krävas för att betala på sista torget (R upp till 64: e kraften, som handlar om 18,446,744,074,000,000,000 — mycket vete faktiskt, säkert mer än i hela riket). Dessa exempel betonar det ofta överraskande sättet på vilket en exponentiell process kan leda till mycket stora antal mycket snabbt.
