snabbt svar:
för en rätvinklig triangel:

sinusfunktionen sin tar vinkel θ och ger förhållandet motsatt hypotenus
den inversa sinusfunktionen sin-1 tar förhållandet motsatthypotenuse och ger vinkel θ
och cosinus och tangent följer en liknande idé.,
och nu för detaljer:
sinus, cosinus och Tangent är alla baserade på en rätvinklig triangel
de är mycket liknande funktioner … så vi kommer att titta på sinusfunktionen och sedan invers sinus för att lära sig vad det handlar om.,
sinusfunktion
Sinusvinkeln θ är:
- längden på sidans motsatta vinkel θ
- dividerat med Hypotenusans längd
eller mer enkelt:
sin(θ) = motsatt/hypotenus
sinusfunktionen kan hjälpa oss att lösa saker som detta:
invers sinusfunktion
men ibland är det den vinkel vi behöver hitta.
det är här ”Inverse sinus” kommer in.
det svarar på frågan ” vilken vinkel har sinus lika med motsatt / hypotenus?,”
symbolen för inverse sinus är sin-1, eller ibland arcsin.
de är som framåt och bakåt!

- sin tar en vinkel och ger oss förhållandet ”motsatt/hypotenus”
- sin-1 tar förhållandet ”motsatt/hypotenus” och ger oss vinkeln.
exempel:
kalkylator
 |
på kalkylatorn trycker du på något av följande (beroende på ditt märke av kalkylator):antingen ’2ndf sin’ eller ’shift sin’. |
på din kalkylator, försök använda sin och sedan sin-1 för att se vad som händer
mer än en vinkel!
Inverse sinus visar bara en vinkel … men det finns fler vinklar som kan fungera.
exempel: här är två vinklar där motsatt / hypotenus = 0.,5
i själva verket finns det oändligt många vinklar, eftersom du kan fortsätta att lägga till (eller subtrahera) 360°:
Kom ihåg detta, eftersom det finns tillfällen när du faktiskt behöver en av de andra vinklarna!
sammanfattning
sinus för vinkel θ är:
sin(θ) = motsatt/hypotenus
och Inverse sinus är:
sin-1 (motsatt/hypotenus) = θ
vad sägs om ”cos” och ”tan” … ?
exakt samma idé, men olika sidokvoter.,
cosinus
cosinus av vinkel θ är:
cos(θ) = intilliggande / hypotenus
och invers cosinus är:
cos-1 (intilliggande / hypotenus) = θ
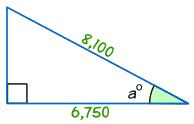
exempel: hitta storleken på vinkeln a°
cos a° = intilliggande / hypotenus
cos a° = 6,750/8,100 = 0,8333…
en° = cos-1 (0.8333…) = 33.,6° (till 1 decimal)
Tangent
tangenten för vinkel θ är:
tan(θ) = motsatt / intilliggande
så omvänd Tangent är :
tan-1 (motsatt / intilliggande) = θ
p>
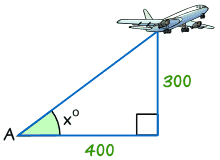
exempel: hitta storleken på vinkel X°
tan x° = motsatt / angränsande
tan x° = 300/400 = 0,75
x° = tan-1 (0,75) = 36.,9° (korrekt till 1 decimal)
andra namn
ibland sin-1 kallas asin eller arcsin
likaså cos-1 kallas acos eller arccos
och tan-1 kallas atan eller arctan
exempel:
- arcsin(y) är densamma som sin-1(y)
- atan(θ) är samma som Tan-1(θ)
- etc.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- men den Inverse sinus och Inverse cosinus ”går inte för evigt” som sinus och cosinus gör …
Låt oss titta på exemplet med cosinus.
Här är cosinus och invers cosinus ritad på samma diagram:
cosinus och invers cosinus
de är spegelbilder (om diagonalen)
men varför blir invers cosinus huggad upptill och ner (prickarna är inte riktigt en del av funktionen) … ?
För att vara en funktion kan den bara ge ett svar
när vi frågar ” Vad är cos-1 (x) ?,”
ett svar eller oändligt många svar
men vi såg tidigare att det finns oändligt många svar, och den streckade linjen på grafen visar detta.
så ja det finns oändligt många svar …
… men tänk dig att du skriver 0.5 i din räknare, tryck cos – 1 och det ger dig en aldrig sinande lista över möjliga svar …
Så vi har denna regel att en funktion bara kan ge ett svar.
så, genom att hugga av det så får vi bara ett svar, men vi bör komma ihåg att det kan finnas andra svar.,
Tangent och invers Tangent
och här är tangent funktionen och invers tangent. Kan du se hur de är spegelbilder (om diagonalen) …?

Tangent

Inverse Tangent



