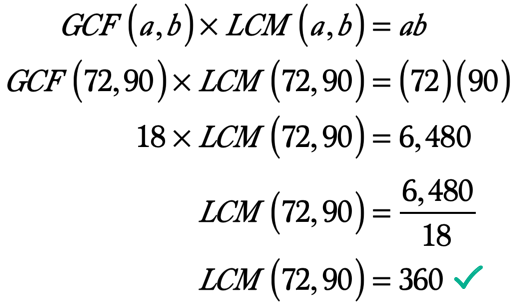När du studerade hur man hittar GCF och LCM av två positiva tal, upptäckte du ett mycket intressant förhållande mellan de två kvantiteterna?

det gjorde jag! Jag upptäckte det av en slump när jag var ung student och jag trodde att jag snubblade på något som var ”revolutionärt”. Jag var så glad att jag delade den med min lärare., Men till min frustration tittade han på mig i ögat och sa att det redan var ett bevisat matematiskt uttalande. Jag kände mig avskräckt ett ögonblick men jag gick tillbaka till mitt skolarbete och tryckte på.

om du inte har stött på det ännu, finns det en anmärkningsvärd algebraisk relation eller länk mellan den största gemensamma faktorn (GCF) och den minst vanliga multipel (LCM) av två siffror. I den här lektionen är de siffror som vi vill ha endast de som tillhör uppsättningen positiva heltal.,
nedan är den algebraiska anslutningen mellan GCF och LCM av två positiva heltal.
GCF-LCM formel
VARNING: Det finns verkligen ingen sådan sak som ”GCF-LCM formel”. Jag hittade bara på namnet för enkel referens. Du kan kalla det vad du vill så länge det tjänar sitt syfte.,
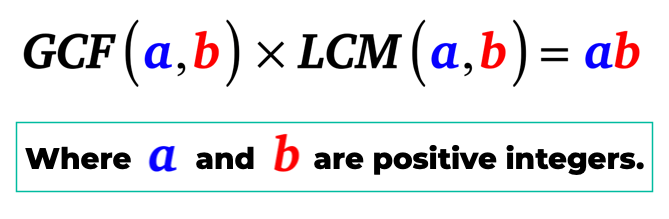
enkelt uttryckt är den största gemensamma faktorn för A och b när den multipliceras med den minst vanliga multipel av A och b lika med produkten av A och B. det vill säga A och B är positiva heltal.
exempelproblem
exempel 1: GCF för 12 och 16 är 4. Vad är LCM av 12 och 16?
Du kan bestämma LCM av 12 och 16 med någon av de två metoderna nedan.,
- att hitta LCM med Listmetoden
- att hitta LCM med Prime Factorization-metoden
det finns dock ett mycket snabbare sätt. Du kan dra nytta av ”GCF-LCM formel” eftersom du vet de två heltal och dess GCF. Bara koppla in värdena i formeln och lösa sedan för LCM.
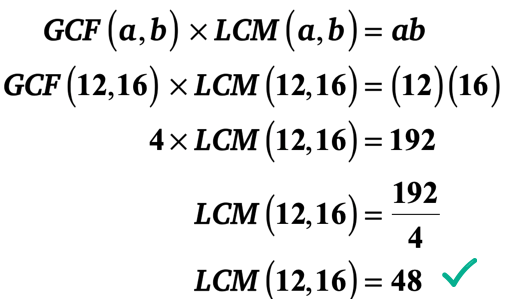
Jag lämnar det till dig för att verifiera att LCM på 12 och 16 faktiskt är 48.
exempel 2: LCM av 24 och 40 är 120. Vad är GCF av 24 och 40?,
det här problemet är exakt motsatsen till exempel 1 eftersom du får värdet på LCM istället för GCF.
så det här är den information som vi vet. Låt oss specificera dem för tydlighet.
▶ mur(24,40) = 120
▶ mur a = 24 och B = 40 därför ab = \ vänster ({24} \ Höger) \Vänster( {40} \ höger) = 960
Obs: Det spelar ingen roll vilka siffror som är A och b. det kommer inte att ändra resultatet av det slutliga svaret. Det är dock en bra praxis att standardisera din lösning. Jag föreslår att du låter en vara mindre heltal medan b vara större heltal.,
låt oss ersätta de kända värdena i formeln och lösa sedan för GCF av 24 och 40.
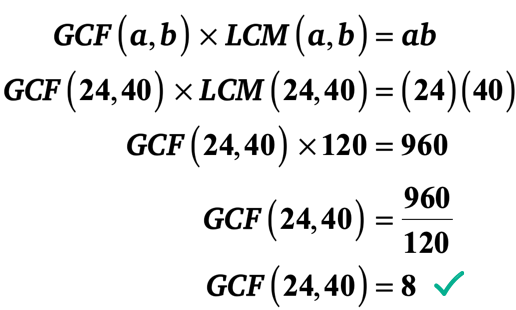
exempel 3: hitta GCF på 20 och 25 genom att först beräkna LCM på 20 och 25.
det här problemet kommer att vara lite annorlunda än Exempel #1 och #2. Du måste först beräkna den minst vanliga multipel (LCM) av 20 och 25. Därefter kan du lösa för den största gemensamma faktorn (GCF) av 20 och 25 genom att använda GCF-LCM-formeln.
Så här går vi!, För att hitta LCM av 20 och 25 kommer vi att skriva de första multiplarna av 20 och 25. Den allra första gemensamma multipel som dyker upp kommer att vara vår LCM.
multiplar av 20: 20, 40, 60, 80, 100, 120
multiplar av 25: 25, 50, 75, 100, 125, 150
eftersom antalet 100 visas som den första gemensamma multipel av 20 och 25, då kan vi hävda att LCM av 20 och 25 är 100.
Vi har nu all information för att använda formeln. Nedan är de värden som vi kommer att ersätta i formeln för att lösa för LCM av 20 och 25.,
◉ produkten av a-och b – → ab = \left( {20} \right)\left( {25} \right) = 500
◉ Den minsta gemensamma multipeln av 20-och 25 – → LCM\left( {20,25} \right) = 100
Här är beräkningen att lösa för GCF av 20-och 25:
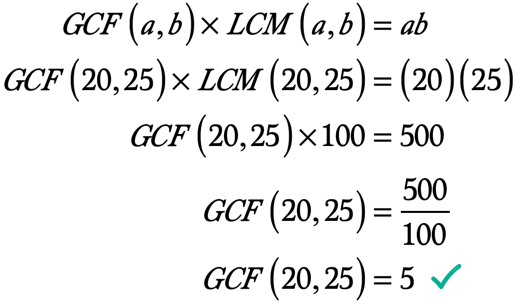
Exempel 4: Hitta den minsta gemensamma multipeln av 63 och 84 genom att först beräkna den gröna klimatfonden 63 och 84.
det här problemet liknar exempel #3. Den enda skillnaden är att du först beräknar GCF istället för LCM, enligt instruktioner från själva problemet.,
låt oss hitta alla faktorer av 63 och 84. Du kan använda” rainbow method ” – tekniken för att faktor de givna heltalen.
Observera att den största eller högsta gemensamma faktorn mellan de två listorna är 21.
faktorer av 63: 1, 3, 7, 9, 21, 63
faktorer av 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
därför är den största gemensamma faktorn 63 och 84 21. Alltså, GCF\left( {63,84} \right) = 21.,
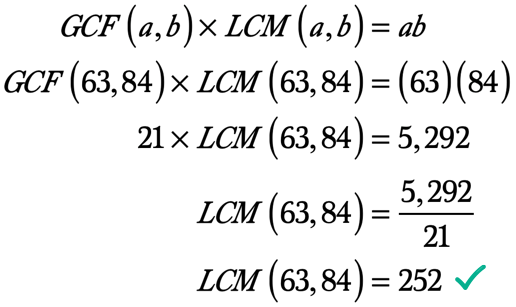
exempel 5: Hitta LCM på 72 och 90 med hjälp av GCF-LCM-formeln.
som vi redan vet kan vi hitta LCM av två heltal med värdet av dess GCF med hjälp av GCF-LCM-formeln.,
listar både faktorerna 72 och 90, vi har:
alla faktorer av 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
alla faktorer av 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
När vi jämför listorna över faktorer ser vi att 18 är den faktor som är gemensam för båda men har det största eller största värdet. Det betyder att GCF av 72 och 90 är 18, det vill säga GCF \ left ({72,90} \right) = 18.
Vi är nu redo att ersätta värdena nedan i formeln.,
mureau ab = \left( {72} \right)\left( {90} \right) = 6,480
GCF\left( {72,90} \right) = 18
här är beräkningen för att hitta LCM med tanke på att vi redan känner till GCF för de två heltalen och deras produkt.