Statistics 2-korrelationskoefficient och Bestämningskoefficient

korrelationskoefficient

hur väl representerar din regressionsekvation
din uppsättning data?
ett sätt att bestämma svaret på denna fråga är att
undersöka korrelationskoefficienten och bestämningskoefficienten.,

kvantiteten r, kallad den linjära korrelationskoefficienten, mäter styrkan och
riktningen för ett linjärt förhållande mellan två variabler. Den linjära korrelationen
koefficienten kallas ibland Pearson produktmoment korrelationskoefficient i
ära av dess utvecklare Karl Pearson.
den matematiska formeln för beräkning är: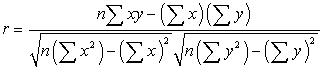

där n är antalet datapar.,
(är du inte glad att du har en grafräknare som beräknar denna formel?)
värdet på r är sådant att -1< r< +1. + Och-tecknen används för positiva
linjära korrelationer respektive negativa linjära korrelationer.
positiv korrelation: om x och y har en stark positiv linjär korrelation är r nära
till +1. Ett R-värde på exakt + 1 indikerar en perfekt positiv passform., Positiva värden
indikerar ett samband mellan X-och y-variabler, så att som värden för X-ökningar ökar
– värdena för y också.
negativ korrelation: om x och y har en stark negativ linjär korrelation är r nära
till -1. Ett R-värde på exakt -1 indikerar en perfekt negativ passform. Negativa värden
anger ett förhållande mellan x och y så att värdena
För y minskar som värden för X-ökning.
ingen korrelation: om det inte finns någon linjär korrelation eller en svag linjär korrelation är r
nära 0., Ett värde nära noll innebär att det finns ett slumpmässigt, olinjärt förhållande
mellan de två variablerna
Observera att r är en dimensionslös mängd; det vill säga det beror inte på enheterna
som används.
en perfekt korrelation av ± 1 uppstår endast när datapunkterna alla ligger exakt på en
rak linje. Om r = + 1 är lutningen på denna linje positiv. Om r = -1 är lutningen på denna
– linje negativ.
en korrelation större än 0.8 beskrivs i allmänhet som stark, medan en korrelation
mindre än 0.,5 beskrivs allmänt somsveka. Dessa värden kan variera beroende på typen
av data som undersöks. En studie som använder vetenskapliga data kan kräva en starkare
korrelation än en studie som använder Samhällsvetenskapliga data.

bestämningskoefficienten, r 2,är användbar eftersom den ger andelen
variansen (fluktuationen) för en variabel som är förutsägbar från den andra variabeln.,
det är en åtgärd som gör det möjligt för oss att bestämma hur säker man kan vara i att göra
förutsägelser från en viss modell/graf.
bestämningskoefficienten är förhållandet mellan den förklarade variationen och den totala
variationen.
bestämningskoefficienten är sådan att 0< r 2< 1, och anger styrkan
för den linjära kopplingen mellan x och y.,
bestämningskoefficienten representerar procentandelen av de data som ligger närmast
till linjen för bästa passform. Till exempel, om r = 0.922, då r 2 = 0.850, vilket innebär att
85% av den totala variationen iny kan förklaras av det linjära förhållandet mellan x
och y (som beskrivs av regressionsekvationen). De övriga 15% av den totala variationen
I y förblir oförklarliga.
bestämningskoefficienten är ett mått på hur väl regressionslinjen
representerar data., Om regressionslinjen passerar exakt genom varje punkt på
scatter-tomten, skulle den kunna förklara all variation. Ju längre linjen är
bort från punkterna, desto mindre kan den förklara.