
i den här artikeln, du kommer att lära dig om SVM eller support vector machine, som är en av de mest populära ai-algoritmerna (det är en av de 10 bästa AI-algoritmerna) och om kärntricket, som handlar om icke-linjäritet och högre dimensioner., Vi kommer att beröra ämnen som hyperplaner, Lagrange multiplikatorer, vi kommer att ha visuella exempel och kodexempel (liknande kodexempel som används i KNN-kapitlet) för att bättre förstå denna mycket viktiga algoritm.
SVM förklarade
Supportvektormaskinen är en övervakad inlärningsalgoritm som oftast används för klassificering, men den kan också användas för regression. Huvudidén är att algoritmen, baserat på de märkta data (träningsdata), försöker hitta den optimala hyperplan som kan användas för att klassificera nya datapunkter. I två dimensioner är hyperplanet en enkel linje.,
vanligtvis försöker en inlärningsalgoritm att lära sig de vanligaste egenskaperna (vad som skiljer en klass från en annan) i en klass och klassificeringen baseras på de representativa egenskaper som man lärt sig (så klassificeringen baseras på skillnader mellan klasser). SVM arbetar tvärtom. Den finner de mest liknande exemplen mellan klasserna. De kommer att vara stödvektorerna.
som ett exempel, låt oss överväga två klasser, äpplen och citroner.,
andra algoritmer kommer att lära sig de mest uppenbara, mest representativa egenskaperna hos äpplen och citroner, som äpplen är gröna och rundade medan citroner är gula och har elliptisk form.
däremot söker SVM efter äpplen som är mycket lik citroner, till exempel äpplen som är gula och har elliptisk form. Detta kommer att vara en stödvektor. Den andra stödvektorn kommer att vara en citron som liknar ett äpple (grön och rundad). Så andra algoritmer lär sig skillnaderna medan SVM lär sig likheter.,
om vi visualiserar exemplet ovan i 2D kommer vi att ha något så här:

När vi går från vänster till höger kommer alla exempel att klassificeras som äpplen tills vi når det gula äpplet. Från denna punkt ökar förtroendet för att ett nytt exempel är ett äpple droppar medan citronklassens förtroende ökar., När citronklassens förtroende blir större än äppelklassens förtroende, kommer de nya exemplen att klassificeras som citroner (någonstans mellan det gula äpplet och den gröna citronen).
baserat på dessa stödvektorer försöker algoritmen hitta det bästa hyperplanet som skiljer klasserna. I 2D är hyperplane en linje, så det skulle se ut så här:

ok, men varför ritade jag den blå gränsen som på bilden ovan?, Jag skulle också kunna rita gränser så här:

som du kan se kan vi se att vi kan dra gränser så här:
ar ett oändligt antal möjligheter att dra beslutsgränsen. Så hur kan vi hitta den optimala?
hitta den optimala Hyperplane
intuitivt den bästa linjen är den linje som är långt ifrån både äpple och citron exempel (har den största marginalen)., För att få optimal lösning måste vi maximera marginalen på båda sätten (om vi har flera klasser måste vi maximera det med tanke på var och en av klasserna).

så om vi jämför bilden ovan med bilden nedan, kan vi enkelt observera att den första är den optimala hyperplanen (linjen) och den andra är en suboptimal lösning, eftersom marginalen är mycket kortare.,

eftersom vi vill maximera marginalerna som tar hänsyn till alla klasser, i stället för att använda en marginal för varje klass använder vi en ”global” marginal, som tar hänsyn till alla klasser., Denna marginal skulle se ut som den lila linjen i följande bild:

denna marginal skulle se ut som den lila linjen i följande bild:
så var har vi vektorer? Var och en av beräkningarna (beräkna avstånd och optimala hyperplaner) görs i vektoriellt utrymme, så varje datapunkt anses vara en vektor. Dimensionen av utrymmet definieras av antalet attribut av exemplen., För att förstå matematiken bakom, läs denna korta matematiska beskrivning av vektorer, hyperplaner och optimeringar: SVM kortfattat.
allt som allt är stödvektorer datapunkter som definierar hyperplanets position och marginal. Vi kallar dem” support ” vektorer, eftersom det här är klassens representativa datapunkter, om vi flyttar en av dem kommer positionen och/eller marginalen att förändras. Att flytta andra datapunkter kommer inte att ha effekt över marginalen eller hyperplanets position.,
för att göra klassificeringar behöver vi inte alla träningsdatapunkter (som i fallet med KNN), vi måste bara spara stödvektorerna. I värsta fall kommer alla punkter att vara stödvektorer, men det här är mycket sällsynt och om det händer, bör du kontrollera din modell för fel eller buggar.
så i princip är lärandet likvärdigt med att hitta hyperplanet med den bästa marginalen, så det är ett enkelt optimeringsproblem.,de grundläggande stegen i SVM är:
- välj två hyperplaner (i 2D) som skiljer data utan punkter mellan dem (röda linjer)
- maximera deras avstånd (marginalen)
- Den genomsnittliga linjen (här linjen halvvägs mellan de två röda linjerna) kommer att vara beslutsgränsen
det här är väldigt trevligt och enkelt, men att hitta den bästa marginalen, optimeringsproblemet är inte trivialt (det är lätt att 2d, när vi bara har två attribut, men vad händer om vi har n dimensioner med n ett mycket stort antal)
för att lösa OPTIMERINGSPROBLEMET använder vi Lagrange-multiplikatorerna., För att förstå denna teknik som du kan läsa de följande två artiklar: Dualitet Langrange Multiplikator och En Enkel Förklaring till Varför Langrange Multiplikatorer Wroks.
hittills hade vi linjärt separerbara data, så vi kunde använda en linje som klassgräns. Men vad händer om vi måste hantera icke-linjära datamängder?,
SVM för icke-linjära datamängder
ett exempel på icke-linjära data är:

i det här fallet kan vi inte hitta en rak linje för att separera äpplen från citroner. Så hur kan vi lösa detta problem. Vi kommer att använda Kärntricket!
grundidén är att när en datamängd är oskiljaktig i de aktuella dimensionerna, Lägg till en annan dimension, kanske så att data kan separeras., Tänk bara på det, exemplet ovan är i 2D och det är oskiljaktigt, men kanske i 3D finns det ett gap mellan äpplen och citronerna, kanske finns det en nivåskillnad, så citroner är på nivå ett och citroner är på nivå två. I det här fallet kan vi enkelt rita en separerande hyperplan (i 3D är ett hyperplan ett plan) mellan nivå 1 och 2.
kartläggning till högre dimensioner
för att lösa detta problem borde vi inte bara blint lägga till en annan dimension, vi borde omvandla utrymmet så att vi genererar denna nivåskillnad avsiktligt.,
kartläggning från 2D till 3D
låt oss anta att vi lägger till en annan dimension som heter X3. En annan viktig omvandling är att i den nya dimensionen är punkterna organiserade med hjälp av denna formel x12 + x22.
om vi plottar det plan som definieras av x2 + y2-formeln får vi något så här:

nu måste vi kartlägga äpplen och citroner (som bara är enkla punkter) till detta nya utrymme. Tänk noga på det, vad gjorde vi?, Vi använde just en omvandling där vi lade till nivåer baserat på avstånd. Om du är i ursprunget kommer poängen att vara på lägsta nivå. När vi rör oss bort från ursprunget betyder det att vi klättrar uppför kullen (rör sig från mitten av planet mot marginalerna) så nivån på punkterna blir högre., Nu om vi anser att ursprunget är citronen från mitten, kommer vi att ha något så här:
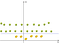
Nu kan vi enkelt separera de två klasserna. Dessa omvandlingar kallas kärnor. Populära kärnor är: Polynomial Kernel, Gaussian Kernel, Radial Basis Function (RBF), Laplace RBF Kernel, Sigmoid Kernel, Anove RBF Kernel, etc (se kärnfunktioner eller en mer detaljerad beskrivning Maskininlärningskärnor).,
kartläggning från 1D till 2D
ett annat, enklare exempel i 2D skulle vara:

efter att ha använt kärnan och efter alla omvandlingar får vi:

så efter omvandlingen kan vi enkelt avgränsa de två klasserna med bara en enda rad.,
i verkliga applikationer kommer vi inte att ha en enkel rak linje, men vi kommer att ha massor av kurvor och höga dimensioner. I vissa fall kommer vi inte att ha två hyperplaner som skiljer data utan punkter mellan dem, så vi behöver några kompromisser, tolerans för avvikare. Lyckligtvis har SVM-algoritmen en så kallad regulariseringsparameter för att konfigurera trade-off och att tolerera outliers.
inställningsparametrar
som vi såg i föregående avsnitt är det viktigt att välja rätt kärna, för om omvandlingen är felaktig kan modellen ha mycket dåliga resultat., Som tumregel, Kontrollera alltid om du har linjära data och använd i så fall alltid linjär SVM (linjär kärna). Linjär SVM är en parametrisk modell, men en RBF-kärna SVM är inte, så komplexiteten hos den senare växer med träningsuppsättningens storlek. Inte bara är dyrare att träna en RBF-kärna SVM, men du måste också hålla kärnmatrisen runt, och projektionen i detta ”oändliga” högre dimensionella utrymme där data blir linjärt separerbara är dyrare också under förutsägelse., Dessutom har du fler hyperparametrar att ställa in, så modellval är dyrare också! Och slutligen är det mycket lättare att överfitta en komplex modell!
regularisering
Regulariseringsparametern (i python kallas det C) berättar SVM-optimeringen hur mycket du vill undvika att missa klassificera varje träningsexempel.
om C är högre, optimeringen kommer att välja mindre marginal hyperplane, så träningsdata missar klassificeringsgraden kommer att vara lägre.,
å andra sidan, om C är låg, kommer marginalen att vara stor, även om det kommer att finnas miss classified training data exempel. Detta visas i följande två diagram:

som du kan se i bilden, när C är låg, är marginalen högre (så implicit har vi inte så många kurvor, linjen följer inte strikt datapunkterna) även om två äpplen klassificerades som citroner., När C är hög är gränsen full av kurvor och alla träningsdata klassificerades korrekt. Glöm inte, även om alla träningsdata var korrekt klassificerade, detta betyder inte att öka C kommer alltid att öka precisionen (på grund av overfitting).
Gamma
nästa viktiga parameter är Gamma. Gamma-parametern definierar hur långt påverkan av ett enda träningsexempel når. Detta innebär att hög Gamma kommer att överväga endast punkter nära den troliga hyperplan och låg Gamma kommer att överväga punkter på större avstånd.,

yperplane kommer att överväga punkter på större avstånd så fler och fler punkter kommer att användas (gröna linjer indikerar vilka punkter som beaktades när man hittade den optimala hyperplanet).
Marginal
den sista parametern är marginalen. Vi har redan talat om marginal, högre marginalresultat bättre modell, så bättre klassificering (eller förutsägelse)., Marginalen ska alltid maximeras.
SVM exempel med Python
i det här exemplet kommer vi att använda Social_Networks_Ads.csv-fil, samma fil som vi använde i föregående artikel, se KNN exempel med Python.
i det här exemplet skriver jag bara ner skillnaderna mellan SVM och KNN, eftersom jag inte vill upprepa mig själv i varje artikel! Om du vill ha hela förklaringen om hur vi kan läsa datauppsättningen, hur analyserar vi och delar upp våra data eller hur kan vi utvärdera eller rita beslutsgränserna, läs sedan kodexemplet från föregående kapitel (KNN)!,
eftersom sklearn-biblioteket är ett mycket välskrivet och användbart Python-bibliotek har vi inte för mycket kod att ändra. Den enda skillnaden är att vi måste importera SVC klass (SVC = SVM i sklearn) från sklearn.svm istället för KNeighborsClassifier klass från sklearn.grannen.
Efter att ha importerat SVC kan vi skapa vår nya modell med den fördefinierade konstruktören. Denna konstruktör har många parametrar, men jag kommer att beskriva bara de viktigaste, för det mesta kommer du inte använda andra parametrar.,
de viktigaste parametrarna är:
- kernel: kärntypen som ska användas. De vanligaste kärnorna är rbf (det här är standardvärdet), poly eller sigmoid, men du kan också skapa din egen kärna.,
- c: det här är regulariseringsparametern som beskrivs i avsnittet Tuning Parameters
- gamma: detta beskrivs också i avsnittet Tuning Parameters
- grad: det används endast om den valda kärnan är poly och anger graden av polinom
- Sannolikhet: det här är en boolesk parameter och om det är sant kommer modellen att återvända för varje förutsägelse, vektorn av sannolikheter att tillhöra varje klass av svarsvariabeln. Så i princip kommer det att ge dig förtroende för varje förutsägelse.,
- krympning: detta visar om du vill ha en krympande heuristisk används i din optimering av SVM, som används i sekventiell Minimal optimering. Det är standardvärdet är sant, en om du inte har en bra anledning, vänligen inte ändra detta värde till falskt, eftersom krympning kommer att avsevärt förbättra din prestanda, för mycket liten förlust när det gäller noggrannhet i de flesta fall.
Nu kan se utgången av att köra denna kod., Beslutsgränsen för träningsuppsättningen ser ut så här:

som vi kan se och som vi har lärt oss i avsnittet inställningsparametrar, eftersom C har ett litet värde (0,1) är beslutsgränsen jämn.
Nu om vi ökar C från 0.,1 till 100 Vi kommer att ha fler kurvor i beslutsgränsen:

vad skulle hända om vi använder C=0.1 men nu ökar vi gamma från 0,1 till 10? Låt se!

vad hände här? Varför har vi en så dålig modell?, Som du har sett i avsnittet inställningsparametrar betyder high gamma att vid beräkning av det trovärdiga hyperplanet betraktar vi bara punkter som är nära. Nu för att densiteten hos de gröna punkterna är hög endast i den valda gröna regionen, i den regionen är punkterna tillräckligt nära det troliga hyperplanet,så de hyperplanerna valdes. Var försiktig med gamma-parametern, eftersom det kan ha ett mycket dåligt inflytande över resultaten av din modell om du ställer in det till ett mycket högt värde (vad är ett ”mycket högt värde” beror på datapunkternas densitet).,
för detta exempel är de bästa värdena för C och Gamma 1,0 och 1,0. Nu om vi kör vår modell på testuppsättningen får vi följande diagram:

och Förvirringsmatrisen ser ut så här:

som du kan se har vi bara 3 falska positiva och endast 4 falska negativa. – herr talman!, Noggrannheten i denna modell är 93% vilket är ett riktigt bra resultat, vi fick en bättre poäng än att använda KNN (som hade en noggrannhet på 80%).
OBS: noggrannhet är inte det enda mätvärdet som används i ML och inte heller det bästa mätvärdet för att utvärdera en modell, på grund av Noggrannhetsparadoxen. Vi använder detta mått för enkelhet, men senare, i kapitlet mätvärden för att utvärdera AI-algoritmer kommer vi att prata om Noggrannhetsparadoxen och jag kommer att visa andra mycket populära mätvärden som används inom detta område.,
slutsatser
i den här artikeln har vi sett en mycket populär och kraftfull övervakad inlärningsalgoritm, Supportvektormaskinen. Vi har lärt oss den grundläggande idén, vad är en hyperplan, vad är stödvektorer och varför är de så viktiga. Vi har också sett massor av visuella representationer, vilket hjälpte oss att bättre förstå alla begrepp.
ett annat viktigt ämne som vi berörde är Kärntricket, vilket hjälpte oss att lösa icke-linjära problem.
för att få en bättre modell såg vi tekniker för att ställa in algoritmen., I slutet av artikeln hade vi ett kodexempel i Python, som visade oss hur kan vi använda KNN-algoritmen.
som slutliga tankar skulle jag vilja ge några fördelar & nackdelar och några populära användningsfall.,
proffsen
- SVN kan vara mycket effektiv, eftersom den endast använder en delmängd av träningsdata, fungerar bara stödvektorerna
- mycket bra på mindre datamängder, på icke-linjära datamängder och högdimensionella utrymmen
- är mycket effektiv i fall där antalet dimensioner är större än antalet prover
- Det kan ha hög noggrannhet, ibland kan prestera ännu bättre än neurala nätverk
- inte särskilt känsliga för att overfitting
cons
- träningstiden är hög när vi har stora datamängder
- när datamängden har mer brus (i.,e. målklasser överlappar) SVM fungerar inte bra
populära användningsfall
- Textklassificering
- detekterar spam
- sentimentanalys
- Aspektbaserad erkännande
- Aspektbaserad erkännande
- handskriven sifferigenkänning
