SVM und Kernel SVM

In diesem Artikel erfahren Sie mehr über SVM oder Support Vector Machine, einer der beliebtesten KI-Algorithmen (einer der Top 10 KI-Algorithmen) und über den Kernel-Trick, der sich mit Nichtlinearität und höheren Dimensionen befasst., Wir werden Themen wie Hyperplanes, Lagrange-Multiplikatoren berühren, wir werden visuelle Beispiele und Codebeispiele (ähnlich dem Codebeispiel im KNN-Kapitel) haben, um diesen sehr wichtigen Algorithmus besser zu verstehen.

SVM Erklärt

Der Support Vector Machine ist ein betreuter Lern-Algorithmus hauptsächlich für die Einstufung aber es kann auch verwendet werden für regression. Die Hauptidee ist, dass der Algorithmus basierend auf den markierten Daten (Trainingsdaten) versucht, die optimale Hyperebene zu finden, mit der neue Datenpunkte klassifiziert werden können. In zwei Dimensionen ist die Hyperplane eine einfache Linie.,

Normalerweise versucht ein Lernalgorithmus, die gebräuchlichsten Merkmale (was eine Klasse von einer anderen unterscheidet) einer Klasse zu lernen, und die Klassifizierung basiert auf den gelernten repräsentativen Merkmalen (daher basiert die Klassifizierung auf Unterschieden zwischen Klassen). Der SVM arbeitet anders herum. Es findet die ähnlichsten Beispiele zwischen Klassen. Dies werden die Unterstützungsvektoren sein.

Betrachten wir als Beispiel zwei Klassen, Äpfel und Zitronen.,

Andere Algorithmen lernen die offensichtlichsten, repräsentativsten Eigenschaften von Äpfeln und Zitronen, wie Äpfel sind grün und abgerundet, während Zitronen gelb sind und elliptische Form haben.

Im Gegensatz dazu sucht SVM nach Äpfeln, die Zitronen sehr ähnlich sind, zum Beispiel Äpfel, die gelb sind und elliptische Form haben. Dies wird ein Unterstützungsvektor sein. Der andere Unterstützungsvektor ist eine Zitrone ähnlich einem Apfel (grün und abgerundet). So lernen andere Algorithmen die Unterschiede, während SVM Ähnlichkeiten lernt.,

Wenn wir das obige Beispiel in 2D visualisieren, haben wir Folgendes:

Wenn wir von links nach rechts gehen, werden alle Beispiele als Äpfel klassifiziert, bis wir den gelben Apfel erreichen. Ab diesem Zeitpunkt sinkt das Vertrauen, dass ein neues Beispiel ein Apfel ist, während das Vertrauen der Zitronenklasse zunimmt., Wenn das Vertrauen in die Zitronenklasse größer wird als das Vertrauen in die Apfelklasse, werden die neuen Beispiele als Zitronen klassifiziert (irgendwo zwischen dem gelben Apfel und der grünen Zitrone).

Basierend auf diesen Unterstützungsvektoren versucht der Algorithmus, die beste Hyperebene zu finden, die die Klassen trennt. In 2D ist die Hyperebene eine Zeile, daher würde sie folgendermaßen aussehen:

Ok, aber warum habe ich die blaue Grenze wie im Bild oben gezeichnet?, Ich könnte auch Grenzen wie folgt zeichnen:

Wie Sie sehen können, haben wir eine unendliche Anzahl von Möglichkeiten, die Entscheidungsgrenze zu ziehen. Wie können wir also den optimalen finden?

Die optimale Hyperplane finden

Intuitiv Die beste Linie ist die Linie, die weit von Apple-und Lemon-Beispielen entfernt ist (hat den größten Rand)., Um eine optimale Lösung zu haben, müssen wir die Marge auf beide Arten maximieren (wenn wir mehrere Klassen haben, müssen wir sie unter Berücksichtigung jeder der Klassen maximieren).

Wenn wir also das Bild oben mit dem Bild unten vergleichen, können wir leicht beobachten, dass die erste die optimale Hyperebene (Linie) und die zweite eine suboptimale Lösung ist, weil die Marge viel kürzer ist.,

Da wir die Ränder unter Berücksichtigung aller Klassen maximieren möchten, anstatt die Ränder mit einem Rand für jede Klasse verwenden wir einen „globalen“ Rand, der alle Klassen berücksichtigt., Dieser Rand würde wie die violette Linie im folgenden Bild aussehen:

Dieser Rand ist orthogonal zur Grenze und äquidistant zu den Stützvektoren.

Wo haben wir Vektoren? Jede der Berechnungen (Entfernung und optimale Hyperebenen berechnen) wird im Vektorraum durchgeführt, sodass jeder Datenpunkt als Vektor betrachtet wird. Die Dimension des Raums wird durch die Anzahl der Attribute der Beispiele definiert., Um die Mathematik dahinter zu verstehen, lesen Sie bitte diese kurze mathematische Beschreibung von Vektoren, Hyperebenen und Optimierungen: SVM Succintly.

Insgesamt sind Stützvektoren Datenpunkte, die die Position und den Rand der Hyperebene definieren. Wir nennen sie „Unterstützungsvektoren“, weil dies die repräsentativen Datenpunkte der Klassen sind, wenn wir einen von ihnen bewegen, ändern sich die Position und/oder der Rand. Das Verschieben anderer Datenpunkte hat keine Auswirkungen auf den Rand oder die Position der Hyperebene.,

Um Klassifikationen vorzunehmen, benötigen wir nicht alle Trainingsdatenpunkte (wie im Fall von KNN), sondern nur die Stützvektoren. Im schlimmsten Fall sind alle Punkte Unterstützungsvektoren, aber das ist sehr selten und wenn es passiert, sollten Sie Ihr Modell auf Fehler oder Fehler überprüfen.

Im Grunde entspricht das Lernen dem Finden der Hyperebene mit der besten Marge, daher handelt es sich um ein einfaches Optimierungsproblem.,/li>

Die grundlegenden Schritte des SVM sind:

1. Wählen Sie zwei Hyperebenen (in 2D), die die Daten ohne Punkte zwischen ihnen trennen (rote Linien)
2. Maximieren Sie ihren Abstand (der Rand)
3. die durchschnittliche Linie (hier die Linie auf halbem Weg zwischen den beiden roten Linien) ist die Entscheidungsgrenze

Dies ist sehr schön und einfach, aber die beste Marge zu finden, das Optimierungsproblem ist nicht trivial (es ist einfach in 2D, wenn wir nur zwei Attribute haben, aber was ist, wenn wir N Dimensionen mit N einer sehr großen Zahl haben)

Um das Optimierungsproblem zu lösen, verwenden wir die Lagrange-Multiplikatoren., Um diese Technik zu verstehen, können Sie die folgenden zwei Artikel lesen: Dualität Langrange Multiplikator und eine einfache Erklärung, warum Langrange Multiplikatoren Wroks.

Bis jetzt hatten wir linear trennbare Daten, so dass wir eine Linie als Klassengrenze verwenden konnten. Aber was ist, wenn wir uns mit nichtlinearen Datensätzen befassen müssen?,

SVM für nichtlineare Datensätze

Ein Beispiel für nichtlineare Daten ist:

In diesem Fall können wir keine gerade Linie finden, um Äpfel von Zitronen zu trennen. Also, wie können wir dieses problem lösen. Wir werden den Kernel-Trick verwenden!

Die Grundidee ist, dass, wenn ein Datensatz in den aktuellen Dimensionen untrennbar ist, eine andere Dimension hinzugefügt wird, möglicherweise die Daten auf diese Weise trennbar sind., Denken Sie nur darüber nach, das obige Beispiel ist in 2D und es ist untrennbar, aber vielleicht gibt es in 3D eine Lücke zwischen den Äpfeln und den Zitronen, vielleicht gibt es einen Niveauunterschied, also sind Zitronen auf Ebene eins und Zitronen sind auf Ebene zwei. In diesem Fall können wir leicht eine trennende Hyperebene (in 3D ist eine Hyperebene eine Ebene) zwischen Ebene 1 und 2 zeichnen.

Zuordnung zu höheren Dimensionen

Um dieses Problem zu lösen, sollten wir nicht nur blind eine weitere Dimension hinzufügen, sondern den Raum transformieren, damit wir diesen Ebenenunterschied absichtlich erzeugen.,

Zuordnung von 2D zu 3D

Nehmen wir an, wir fügen eine weitere Dimension namens X3 hinzu. Eine weitere wichtige Transformation ist, dass in der neuen Dimension die Punkte mit dieser Formel x12 + x22 organisiert werden.

Wenn wir die durch die Formel x2 + y2 definierte Ebene zeichnen, erhalten wir Folgendes:

Jetzt müssen wir die Äpfel und Zitronen (die nur einfache Punkte sind) diesem neuen Raum zuordnen. Denken Sie sorgfältig darüber nach, was haben wir getan?, Wir haben gerade eine Transformation verwendet, bei der wir Ebenen basierend auf der Entfernung hinzugefügt haben. Wenn Sie im Ursprung sind, befinden sich die Punkte auf der untersten Ebene. Wenn wir uns vom Ursprung entfernen, bedeutet dies, dass wir den Hügel hinaufsteigen (von der Mitte der Ebene zu den Rändern), sodass das Niveau der Punkte höher ist., Wenn wir nun bedenken, dass der Ursprung die Zitrone von der Mitte ist, haben wir ungefähr Folgendes:

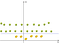
Jetzt können wir die beiden Klassen leicht trennen. Diese Transformationen werden Kernel genannt. Beliebte Kernel sind: Polynomkern, Gauß-Kernel, Radial Basis-Funktion (RBF), Laplace RBF Kernel, Sigmoid Kernel, Anove RBF Kernel, etc (siehe Kernel-Funktionen oder eine detailliertere Beschreibung Maschinelles Lernen Kernel).,

Zuordnung von 1D zu 2D

Ein anderes, einfacheres Beispiel in 2D wäre:

Nach der Verwendung des Kernels und nach allen Transformationen erhalten wir:

Nach der Transformation können wir die beiden Klassen einfach mit nur einer einzigen Zeile abgrenzen.,

In realen Anwendungen werden wir keine einfache gerade Linie haben, aber wir werden viele Kurven und hohe Abmessungen haben. In einigen Fällen werden wir nicht zwei Hyperebenen haben, die die Daten ohne Punkte zwischen ihnen trennt, also brauchen wir einige Kompromisse, Toleranz für Ausreißer. Glücklicherweise verfügt der SVM-Algorithmus über einen sogenannten Regularisierungsparameter, um den Kompromiss zu konfigurieren und Ausreißer zu tolerieren.

Tuning Parameter

Wie wir im vorherigen Abschnitt gesehen haben, ist die Auswahl des richtigen Kernels entscheidend, denn wenn die Transformation falsch ist, kann das Modell sehr schlechte Ergebnisse haben., Überprüfen Sie als Faustregel immer, ob Sie lineare Daten haben, und verwenden Sie in diesem Fall immer lineares SVM (linearer Kernel). Linear SVM ist ein parametrisches Modell, ein RBF-Kernel-SVM jedoch nicht, sodass die Komplexität des letzteren mit der Größe des Trainingssatzes zunimmt. Das Trainieren eines RBF-Kernel-SVM ist nicht nur teurer, sondern Sie müssen auch die Kernmatrix beibehalten, und die Projektion in diesen „unendlichen“ höherdimensionalen Raum, in dem die Daten linear trennbar werden, ist auch während der Vorhersage teurer., Darüber hinaus müssen Sie mehr Hyperparameter einstellen, sodass die Modellauswahl auch teurer ist! Und schließlich ist es viel einfacher, ein komplexes Modell zu überfit!

Regularisierung

Der Regularisierungsparameter (in Python heißt er C) teilt der SVM-Optimierung mit, wie viel Sie vermeiden möchten, dass jedes Trainingsbeispiel nicht klassifiziert wird.

Wenn die C ist höher, die optimierung wird wählen kleinere marge hyperplane, so ausbildung daten verpassen klassifizierung rate wird niedriger sein.,

Auf der anderen Seite, wenn die C niedrig ist, dann wird die Marge groß sein, auch wenn es einige klassifizierte Trainingsdaten Beispiele. Dies wird in den folgenden zwei Diagrammen gezeigt:

Wie Sie im Bild sehen können, wenn das C niedrig ist, ist der Rand höher (so implizit haben wir nicht so viele Kurven, die Linie folgt nicht streng den Datenpunkten), selbst wenn zwei Äpfel als Zitronen klassifiziert wurden., Wenn das C hoch ist, ist die Grenze voller Kurven und alle Trainingsdaten wurden korrekt klassifiziert. Vergessen Sie nicht, dass selbst wenn alle Trainingsdaten korrekt klassifiziert wurden, dies nicht bedeutet, dass das Erhöhen des C immer die Genauigkeit erhöht (aufgrund von Überanpassungen).

Gamma

Die nächste wichtige parameter ist Gamma. Der Gamma-Parameter legt fest, wie weit der Einfluss eines einzelnen Trainingsbeispiels reicht. Dies bedeutet, dass High Gamma nur Punkte in der Nähe der plausiblen Hyperebene berücksichtigt und Low Gamma Punkte in größerer Entfernung berücksichtigt.,

Wie Sie sehen können, führt das Verringern des Gammas dazu, dass die richtige Hyperebene gefunden wird betrachten Sie Punkte in größeren Entfernungen, damit immer mehr Punkte verwendet werden (grüne Linien zeigen an, welche Punkte beim Finden der optimalen Hyperebene berücksichtigt wurden).

Rand

Der Letzte parameter ist der Rand. Wir haben bereits über Marge, höhere Marge, besseres Modell, also bessere Klassifizierung (oder Vorhersage) gesprochen., Die Marge sollte immer maximiert werden.

SVM-Beispiel mit Python

In diesem Beispiel verwenden wir Social_Networks_Ads.csv-Datei, die gleiche Datei wie im vorherigen Artikel, siehe KNN-Beispiel mit Python.

In diesem Beispiel werde ich nur die Unterschiede zwischen SVM und KNN aufschreiben, da ich mich nicht in jedem Artikel wiederholen möchte! Wenn Sie die gesamte Erklärung darüber wünschen, wie wir den Datensatz lesen, wie wir unsere Daten analysieren und aufteilen oder wie wir die Entscheidungsgrenzen auswerten oder darstellen können, lesen Sie bitte das Codebeispiel aus dem vorherigen Kapitel (KNN)!,

Da die Sklearn-Bibliothek eine sehr gut geschriebene und nützliche Python-Bibliothek ist, müssen wir nicht zu viel Code ändern. Der einzige Unterschied besteht darin, dass wir die SVC-Klasse (SVC = SVM in sklearn) aus sklearn importieren müssen.svm statt der Knighborsclassifier-Klasse von sklearn.benachbart.

Nach dem Import der SVC können wir unser neues Modell mit dem vordefinierten Konstruktor erstellen. Dieser Konstruktor hat viele Parameter, aber ich werde nur die wichtigsten beschreiben, meistens verwenden Sie keine anderen Parameter.,

Die wichtigsten Parameter sind:

1. kernel: der zu verwendende Kerneltyp. Die häufigsten Kernel sind rbf (dies ist der Standardwert), poly oder sigmoid, aber Sie können auch Ihren eigenen Kernel erstellen.,
2. C: Dies ist der Regularisierungsparameter, der im Abschnitt Abstimmparameter beschrieben wird
3. gamma: Dies wurde auch im Abschnitt Abstimmparameter beschrieben
4. Grad: Es wird nur verwendet, wenn der gewählte Kernel poly ist und den Grad der polinom
5. Wahrscheinlichkeit festlegt: Dies ist ein boolescher Parameter, und wenn es wahr ist, gibt das Modell für jede Vorhersage den Vektor der Wahrscheinlichkeiten zurück, zu jeder Klasse der Antwortvariablen zu gehören. Im Grunde gibt es Ihnen also das Vertrauen für jede Vorhersage.,
6. Schrumpfen: Dies zeigt an, ob eine schrumpfende Heuristik für die Optimierung des SVM verwendet werden soll oder nicht, die für die sequentielle minimale Optimierung verwendet wird. Der Standardwert ist true, und wenn Sie keinen guten Grund haben, ändern Sie diesen Wert bitte nicht in false, da das Schrumpfen Ihre Leistung erheblich verbessert, was in den meisten Fällen zu einem sehr geringen Genauigkeitsverlust führt.

Jetzt können Sie die Ausgabe dieses Codes sehen., Die Entscheidungsgrenze für den Trainingssatz sieht folgendermaßen aus:

Wie wir sehen können und wie wir in der Tuning Parameter abschnitt, weil die C hat eine kleine wert (0,1) die entscheidung grenze ist glatt.

Nun, wenn wir das C von 0 erhöhen.,1 bis 100 Wir werden mehr Kurven in der Entscheidungsgrenze haben:

Was würde passieren, wenn wir C=0.1 verwenden, aber jetzt Gamma von 0,1 auf 10 erhöhen? Mal sehen!

Was ist hier passiert? Warum haben wir so ein schlechtes Modell?, Wie Sie im Abschnitt Tuning-Parameter gesehen haben, bedeutet High Gamma, dass wir bei der Berechnung der plausiblen Hyperebene nur Punkte berücksichtigen, die nahe beieinander liegen. Da nun die Dichte der grünen Punkte nur in der ausgewählten grünen Region hoch ist, sind die Punkte in dieser Region nahe genug an der plausiblen Hyperebene, so dass diese Hyperebenen ausgewählt wurden. Seien Sie vorsichtig mit dem Gamma-Parameter, da dies einen sehr schlechten Einfluss auf die Ergebnisse Ihres Modells haben kann, wenn Sie es auf einen sehr hohen Wert einstellen (was ein „sehr hoher Wert“ ist, hängt von der Dichte der Datenpunkte ab).,

Für dieses Beispiel sind die besten Werte für C und Gamma 1.0 und 1.0. Wenn wir nun unser Modell auf dem Testset ausführen, erhalten wir das folgende Diagramm:

Und die Verwirrungsmatrix sieht so aus dies:

Wie Sie sehen können, haben wir nur 3 falsch Positive und nur 4 Falsch Negative., Die Genauigkeit dieses Modells beträgt 93%, was ein wirklich gutes Ergebnis ist, wir haben eine bessere Punktzahl erzielt als mit KNN (die eine Genauigkeit von 80% hatte).

HINWEIS: Genauigkeit ist nicht die einzige Metrik, die in ML verwendet wird, und aufgrund des Genauigkeitsparadoxons auch nicht die beste Metrik zur Bewertung eines Modells. Wir verwenden diese Metrik der Einfachheit halber, aber später werden wir im Kapitel Metriken zur Bewertung von KI-Algorithmen über das Genauigkeitsparadoxon sprechen und andere sehr beliebte Metriken zeigen, die in diesem Bereich verwendet werden.,

Schlussfolgerungen

In diesem Artikel haben wir einen sehr beliebten und leistungsstarken Algorithmus für überwachtes Lernen gesehen, die Support Vector Machine. Wir haben die Grundidee gelernt, was eine Hyperebene ist, was Unterstützungsvektoren sind und warum sie so wichtig sind. Wir haben auch viele visuelle Darstellungen gesehen, die uns geholfen haben, alle Konzepte besser zu verstehen.

Ein weiteres wichtiges Thema, das wir berührt haben, ist der Kernel-Trick, der uns geholfen hat, nichtlineare Probleme zu lösen.

Um ein besseres Modell zu haben, haben wir Techniken gesehen, um den Algorithmus abzustimmen., Am Ende des Artikels hatten wir ein Codebeispiel in Python, das uns zeigte, wie wir den KNN-Algorithmus verwenden können.

Als letzte Gedanken möchte ich einige Profis & Nachteile und einige beliebte Anwendungsfälle geben.,

<

1. SVN kann sehr effizient sein, da es nur eine Teilmenge der Trainingsdaten verwendet, nur die Stützvektoren
2. Funktioniert sehr gut auf kleineren Datensätzen, auf nichtlinearen Datensätzen und hochdimensionalen Räumen
3. Ist sehr effektiv in Fällen, in denen die Anzahl der Dimensionen größer ist als die Anzahl der Proben
4. Es kann eine hohe Genauigkeit haben, manchmal sogar besser als neuronale Netze
5. Nicht sehr empfindlich auf Überanpassung
6. /li>

Cons

1. Die Trainingszeit ist hoch, wenn wir große Datensätze haben
2. Wenn der Datensatz mehr Rauschen aufweist (i.,e. Ziel-Klassen überlappen) SVM nicht gut

Popular Use Cases

1. Text-Klassifizierung
2. Spamschutz
3. Sentiment-Analyse
4. Aspekt-basierte Erkennung
5. Aspekt-basierte Erkennung
6. Handschriftlichen digit recognition