Der einfachste Weg, um die Idee einer wachsenden Bevölkerung zu erfassen ist mit einem einzelligen Organismus, wie ein Bakterium oder ein cilliate. In Abbildung 1 ist eine Population von Paramecium in einer kleinen Labordepressionsfolie abgebildet. In dieser Population teilen sich die Individuen einmal pro Tag. Also, beginnend mit einer einzelnen Person am Tag 0, wir erwarten, in aufeinanderfolgenden Tagen, 2, 4, 8, 16, 32, und 64 Personen in der Bevölkerung., Wir können hier sehen, dass an einem bestimmten Tag die Anzahl der Personen in der Bevölkerung einfach doppelt so hoch ist wie am Vortag, daher ist die Zahl heute, nennen wir sie N(heute), gleich der doppelten Zahl gestern, nennen wir sie N(gestern), die wir kompakter als N(heute) = 2N(gestern) schreiben können.
Daher ist es sinnvoll, dies als N(t) = 2N(t – 1) zu schreiben, wobei t überhaupt einen beliebigen Wert annehmen könnte.,
Jetzt können wir diese Idee ein wenig verallgemeinern, wenn wir feststellen, dass die Zahl am Tag sechs gleich der doppelten Zahl am Tag fünf oder N(6) = 2N(5) ist und am Tag fünf ist die Zahl gleich der doppelten Zahl am Tag vier oder N(5) = 2N(4) usw.
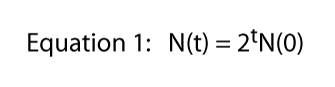
wobei t für eine beliebige Zeit steht (z. B. wenn t = 6, N(6) = 26).
Schließlich stellen wir fest, dass diese Gleichung aus der spezifischen Situation in Abbildung 1 abgeleitet wurde, in der eine Division pro Tag die harte und schnelle Regel war., Hier kommt die 2 in Gleichung 1 her — von jedem einzelnen Paramecium erhalten wir am nächsten Tag zwei Individuen. Natürlich könnte die Teilungsrate alles sein. Wenn es zwei Divisionen pro Tag gäbe, aber immer eine Zelle starb, würden wir von jedem einzelnen Individuum drei Individuen erwarten und Gleichung 1 wäre N(t) = 3tN(0)., Die Teilungsrate könnte also überhaupt eine beliebige Zahl sein und die allgemeine Gleichung lautet:
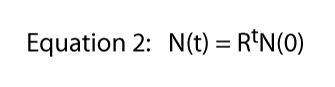
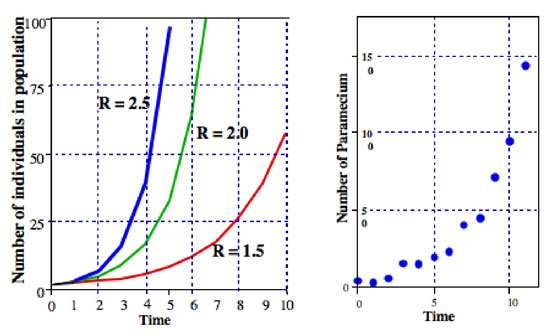
wobei R normalerweise als endliche Rate der Bevölkerungszunahme bezeichnet wird (im tatsächlichen Fall der Teilung von Paramecium ist die endliche Rate der Bevölkerungszunahme gleich der Teilungsrate). In Abbildung 2 veranschaulichen wir diese Gleichung für verschiedene Werte von R. Sie wird normalerweise als Exponentialgleichung bezeichnet, und die Form der Daten in Abbildung 2 ist die allgemeine Form, die als exponentiell bezeichnet wird.,
Jeder Wert von R kann auf unendlich viele Arten dargestellt werden (z. B. wenn R = 16 ist, könnten wir R = 8 x 2 oder R = 42 oder R = 32/2 oder R = 2.718282.77 schreiben). Das Letzte Ausdruck (R = 2.718282.,77) verwendet eine wichtige Konstante, die aus der Elementarrechnung, der Eulerschen Konstante, abgerufen werden kann. Es ist tatsächlich äußerst nützlich, den Wert von R als Eulers Konstante auszudrücken, die auf eine gewisse Kraft angehoben wird — es bringt die volle Kraft der Kalkulation ins Bild.,olize Eulers Konstante als e Wir können Gleichung 2 als
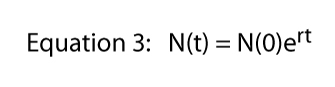
Wenn wir nun das natürliche Protokoll beider Seiten von Gleichung 3 nehmen — denken Sie daran, ln(ex) = x — Gleichung 3 wird: ln = ln + rt
Und wenn wir die Population mit einer einzelnen Person beginnen (wie im obigen Beispiel), haben wir

aus dem wir sehen, dass das natürliche Protokoll der Population zu einem bestimmten Zeitpunkt zu diesem Zeitpunkt konstant ist., Die Konstante r wird als die intrinsische Rate des natürlichen Anstiegs bezeichnet (Abbildung 2).
Alle Arten von Mikroorganismen weisen Muster auf, die dem exponentiellen Bevölkerungswachstum sehr nahe kommen. In der rechten Grafik von Abbildung 2 befindet sich beispielsweise eine Population von Paramecium, die in einer Laborkultur wächst. Das Wachstumsmuster ist dem Muster der Exponentialgleichung sehr nahe.
Eine andere Art, die Exponentialgleichung zu schreiben, ist eine Differentialgleichung, dh die das Wachstum der Bevölkerung in ihrer dynamischen Form darstellt., Anstatt zu fragen, wie groß die Population zum Zeitpunkt t ist, fragen wir, mit welcher Rate die Population zum Zeitpunkt t wächst. Die Rate wird als dN/dt symbolisiert, was einfach „Änderung in N relativ zur Änderung in t“ bedeutet, und wenn Sie sich an Ihre Grundrechnung erinnern, können wir die Wachstumsrate finden, indem wir Gleichung 4 differenzieren, die uns
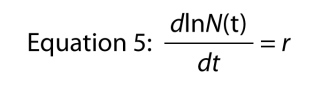
was bemerkenswert ist, weil es sagt, dass die Wachstumsrate des Protokolls der Zahl in der Bevölkerung konstant ist., Diese konstante Wachstumsrate des Stammes der Bevölkerung ist die intrinsische Wachstumsrate.,
Denken Sie daran, dass die Änderungsrate des Protokolls einer Zahl mit der Änderung dieser Zahl „pro Kopf“ identisch ist, was bedeutet, dass wir Gleichung 5 als


iv geht, und dann ordnen wir ein bisschen neu an, um
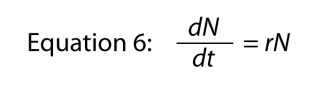
wobei der Parameter r wiederum die intrinsische Rate des natürlichen Anstiegs ist., Die grundlegende Beziehung zwischen endlicher Steigerungsrate und intrinsischer Rate ist
r = ln(R)
wobei ln sich auf den natürlichen Logarithmus bezieht. Beachten Sie, dass Gleichung 6 und Gleichung 3 nur verschiedene Formen derselben Gleichung sind (Gleichung 3 ist die integrierte Form von Gleichung 6; Gleichung 6 ist die differenzierte Form von Gleichung 3), und beide können einfach als Exponentialgleichung bezeichnet werden.,

Die Exponentialgleichung ist zumindest für relativ kurze Zeiträume ein nützliches Modell einfacher Populationen., Wenn beispielsweise ein Labortechniker wissen muss, wann eine Bakterienkultur eine bestimmte Populationsdichte erreicht, kann die Exponentialgleichung verwendet werden, um eine Vorhersage darüber zu geben, wann genau diese Populationsgröße erreicht wird. Ein anderes Beispiel ist bei landwirtschaftlichen Schädlingen. Pflanzenfresser sind immer potenziell große Probleme für Pflanzen. Wenn es sich bei den Pflanzen, die solchen Ausbrüchen ausgesetzt sind, um landwirtschaftliche, dh pflanzliche Pflanzen handelt, kann der Verlust sowohl für Landwirte als auch für Verbraucher sehr bedeutsam sein. Daher besteht immer Druck, solche Ausbrüche zu verhindern., Seit dem Zweiten Weltkrieg waren chemische Pestizide wie DDT die Hauptwaffe bei der Bekämpfung solcher Schädlingsausbrüche. In den letzten Jahren haben wir jedoch festgestellt, dass diese Pestizide auf lange Sicht sowohl für die Umwelt als auch für die Menschen äußerst gefährlich sind. Folglich gab es eine Bewegung, um die Menge an Pestiziden zu begrenzen, die zur Bekämpfung von Schädlingen gesprüht werden. Dies geschieht hauptsächlich durch die Festlegung einer wirtschaftlichen Schwelle, d. H. Der Bevölkerungsdichte des potenziellen Schädlings, unter der der Ernteschaden unbedeutend ist (d. H. Es ist nicht wirklich notwendig zu sprühen)., Wenn die Schädlingspopulation über diese Schwelle steigt, muss der Landwirt Maßnahmen ergreifen und eine Art Pestizid oder andere Mittel zur Schädlingsbekämpfung anwenden. Angesichts der Natur dieses Problems ist es manchmal von größter Bedeutung, vorhersagen zu können, wann der Schädling die wirtschaftliche Schwelle erreichen wird. Die Kenntnis des R für die Schädlingsart ermöglicht es dem Landwirt vorherzusagen, wann ein Kontrollverfahren erforderlich sein wird (Abbildung 3).
Die Exponentialgleichung ist auch ein nützliches Modell für die Entwicklung intuitiver Vorstellungen über Populationen., Das klassische Beispiel ist ein Teich mit einer Bevölkerung von lily pads. Wenn sich jedes Lilienpolster jeden Monat selbst reproduziert (zwei Pads nehmen den Platz ein, an dem sich ein Pad befand), und es beispielsweise drei Jahre dauerte, bis der Teich zur Hälfte mit Lilienpolstern gefüllt war, wie lange dauert es, bis der Teich vollständig mit Lilienpolstern bedeckt ist? Wenn Sie nicht aufhören, zu klar zu denken, ist es verlockend zu sagen, dass es drei Jahre dauern wird, bis die zweite Hälfte des Teiches so gefüllt ist wie die erste. Die Antwort ist natürlich ein Monat.,
Ein weiteres beliebtes Beispiel ist der sprichwörtliche altägyptische (oder manchmal persische) Mathematiker, der vom König die Zahlung in Form von Weizenkörnern (manchmal Reis) verlangt. Ein Korn auf dem ersten Platz eines Schachbretts, zwei Körner auf dem zweiten Platz und so weiter bis zum letzten Platz. Der Pharao kann sich nicht vorstellen, dass eine so einfache Zahlung viel betragen könnte, und stimmt zu. Aber er schätzte das exponentielle Wachstum nicht vollständig., Da es 64 Quadrate auf dem Schachbrett gibt, können wir Gleichung 2 verwenden, um zu bestimmen, wie viele Weizenkörner auf dem letzten Quadrat bezahlt werden müssen (R erhöht auf die 64.Potenz, die etwa 18.446.744.074.000.000.000 ist — eine Menge Weizen in der Tat, sicherlich mehr als im ganzen Königreich). Diese Beispiele unterstreichen die oft überraschende Art und Weise, wie ein exponentieller Prozess sehr schnell zu sehr großen Zahlen führen kann.
