sekvens
en sekvens er et sæt ting (normalt tal), der er i orden.
geometriske sekvenser
i en geometrisk sekvens findes hvert udtryk ved at multiplicere det foregående udtryk med en konstant.
generelt skriver vi en geometrisk sekvens som denne:
{a, ar, ar2, ar3, …, }
hvor:
- a er det første udtryk, og
- r er faktoren mellem udtrykkene (kaldet “common ratio”)
men vær forsigtig, r skal ikke være 0:
- når r=0 får vi sekvensen {a, 0,0,…} som ikke er geometrisk
Den Regel,
Vi kan også beregne nogen sigt ved hjælp af Reglen:
xn = ar(n-1)
(Vi bruger “n-1”, fordi ar0 er for 1. semester)
En Geometrisk Sekvens kan også have mindre og mindre værdier:
Eksempel:
4, 2, 1, 0.5, 0.25, …,
denne sekvens har en faktor på 0,5 (en halv) mellem hvert tal.
dens regel ernn = 4? (0.5)n-1
hvorfor “geometrisk” sekvens?,
fordi det er som at øge dimensionerne i geometri:
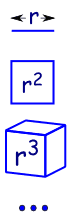 |
en linje er 1-dimensionel og har en længde på r |
| i 2 dimensioner har en firkant et areal på R2 | |
| i 3 dimensioner har en terning volumen R3 | |
| osv. (Ja Vi kan have 4 og flere dimensioner i matematik)., |
Geometriske Sekvenser, der nogle gange kaldes Geometrisk Progressioner (G. P. ‘ s)
Summere en Geometrisk Række
for At opsummere disse:
a + ar + ar2 + … + ar(n-1)
(hvert udtryk er ark, hvor k starter ved 0 og går op til n-1)
Vi kan bruge denne praktiske formel:

A er det første udtryk
r er det “almindelige forhold” mellem udtryk
n er antallet af udtryk
Hvad er det sjove symbol-symbol?, Det kaldes Sigma Notation
| (kaldet Sigma) betyder “sum up” |
og under og over det vises start-og slutværdierne:
Der står “opsummere n hvor n går fra 1 til 4. Svar=10
formlen er nem at bruge …, bare “plug in” værdier for a, r og n
ved Hjælp af Formlen
Lad os se formlen i aktion:
Eksempel: Riskorn på et skakbræt

På siden Binære Cifre giver vi et eksempel på riskorn på et skakbræt. Spørgsmålet er, spurgte:
Når vi placerer ris på et skakbræt:
- 1 korn på første pladsen,
- 2-korn på anden pladsen,
- 4 kerner på den tredje og så videre,
- …
… fordobling af riskornene på hver firkant …
…, hvor mange korn ris i alt?
Så har vi:
- a = 1 (første periode)
- r = 2 (fordobler hver gang)
- n = 64 (64 felter på et skakbræt)
Så:

Bliver:
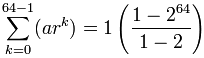
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
Der var præcis det resultat, vi fik i den Binære Cifre side (gudskelov!)
og et andet eksempel, denne gang med r mindre end 1:
Hvorfor virker formlen?,
lad os se, hvorfor formlen fungerer, fordi vi kommer til at bruge et interessant “trick”, som er værd at vide.
Bemærk at S og S·r er ens?
nu trække dem!
Wow! Alle vilkår i midten pænt annullere ud.,
(hvilket er et pænt trick)
Ved at trække S·r fra S får vi et simpelt resultat:
S − s·r = a − arn
lad os omarrangere det for at finde S:
ivider med (1−r):s = a(1−rn)(1−R)
som er vores formel (ta-da!):

uendelig geometrisk serie
Så hvad sker der, når n går til uendelig?,
Vi kan bruge denne formel:
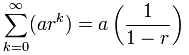
Men vær forsigtig:
r skal være mellem (men ikke inklusive) -1 og 1
og f bør ikke være 0, fordi sekvensen {a,0,0,…} er ikke geometrisk
så vores infnite geometriske serie har en endelig sum, når forholdet er mindre end 1 (og større end -1)
lad os bringe vores tidligere eksempel tilbage, og se hvad der sker:
|
tro mig ikke? Bare se på denne firkant: Ved at tilføje 12 + 14 + 18 + … vi ender med det hele!, |
 |
tilbagevendende Decimal
på en anden side spurgte vi “gør 0.999… lige 1?”, lad os se, om vi kan beregne det:



