Den nemmeste måde at fange idéen om en voksende befolkning med et encellede organisme, som en bakterie eller en cilliate. I Figur 1, en population af Paramecium i et lille laboratoriedepressionsglas er afbildet. I denne befolkning deler individerne en gang om dagen. Så, starter med et enkelt individ på dag 0, Vi forventer, i på hinanden følgende dage, 2, 4, 8, 16, 32, og 64 personer i befolkningen., Vi kan her se, at på en bestemt dag, antallet af individer i populationen er simpelthen det dobbelte af, hvad den var dagen før, så antallet i dag, kalder det at N(i dag), svarende til det dobbelte af antallet i går, kalder det at N(i går), som vi kan skrive mere kompakt som det er N(i dag) = 2N(i går).
så det giver mening at skrive dette som, N(t) = 2N(t – 1), Hvor t overhovedet kunne påtage sig nogen værdi.,
Nu kan vi generalisere denne idé en smule, hvis vi konstatere, at på dag seks antallet er lig med to gange på dag fem, eller N(6) = 2N(5) og på dag fem i antal svarende til det dobbelte af antallet i dag fire, eller N(5) = 2N(4), osv.
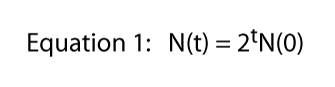
hvor t står til enhver tid på alle (fx, hvis t = 6, N(6) = 26).
endelig bemærker vi, at denne ligning blev afledt af den specifikke situation vist i Figur 1, hvor en division pr., Det er her 2 kommer fra i ligning 1 – fra hvert enkelt Paramecium får vi to individer Den næste dag. Selvfølgelig kan divisionsraten være noget. Hvis der var to divisioner om dagen, men en celle altid døde, ville vi forvente tre individer fra hvert enkelt individ, og ligning 1 ville være n(t) = 3tN(0)., Så division sats kan være mange, og den generelle ligning bliver
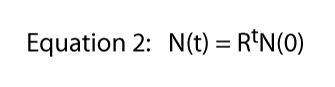
hvor R er normalt kaldet den begrænsede andel af befolkningen stigning i det faktiske tilfælde af at dividere Paramecium finite sats af befolkningstilvækst, er lig med den division sats). I figur 2 illustrerer vi denne ligning for forskellige værdier af R. Det kaldes normalt den eksponentielle ligning, og formen af dataene i figur 2 er den generelle form kaldet eksponentiel.,
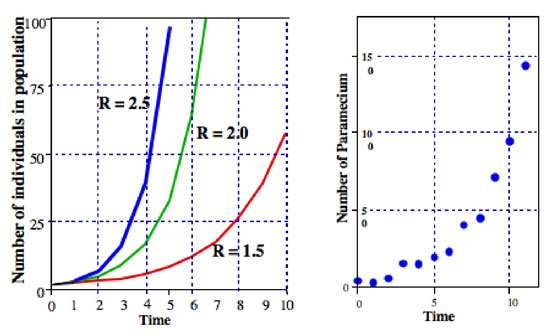
enhver værdi af R kan repræsenteres på et uendeligt antal måder (f if hvis R = 16, kunne vi skrive R = 8.2, eller R = 42, eller R = 32/2, eller R = 2.718282.77). Det sidste udtryk (R = 2.718282.,77) gør brug af en vigtig konstant, der kan erindres fra elementær calculus, Eulers konstant. Udtrykke uanset værdien af R som Eulers konstant hævet til nogle magt er faktisk yderst nyttigt-det bringer den fulde effekt af calculus ind i billedet.,oli Cane Eulers konstant som e vi kan skrive ligning 2 som
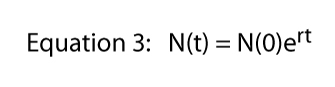
nu, hvis vi tager den naturlige log på begge sider af ligning 3 — husk ln(E becomes) = Equation — ligning 3 bliver: ln = ln + rt
og hvis vi begyndte befolkningen med et enkelt individ (som i eksemplet ovenfor), har vi

nhver bestemt tid, er nogle konstant, gange den tid., Den konstante r betegnes som den iboende hastighed af naturlig stigning (figur 2).
alle slags mikroorganismer udviser mønstre, der er meget tæt på eksponentiel befolkningstilvækst. For eksempel er i højre graf i figur 2 en population af Paramecium, der vokser i en laboratoriekultur. Vækstmønsteret er meget tæt på mønsteret for den eksponentielle ligning.
en anden måde at skrive den eksponentielle ligning på er som en differentialligning, det vil sige at repræsentere befolkningens vækst i sin dynamiske form., Snarere end at spørge, hvad er størrelsen af den befolkning, der på tidspunkt t, kan vi spørge, hvad er den hastighed, hvormed populationen vokser til tiden t. Den sats, der er symboliseret som dN/dt, som blot betyder “ændring i N i forhold til at ændre i t,” og hvis du husker dit grundlæggende calculus, vi kan finde væksten ved at differentiere Ligning 4, hvilket giver os
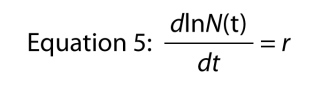
som er en slags bemærkelsesværdig, fordi den siger, at væksten af log af antal i befolkningen er konstant., Denne konstante vækstrate af log af befolkningen er den iboende stigningstakt.,
husk på, at graden af ændring af log af et tal er det samme som “per indbygger” ændring i det antal, hvilket betyder, at vi kan skrive Ligning 5

hvor kan vi udelade den variable t, da det er indlysende, hvor det går, og så er vi omarrangere en smule til at komme op med
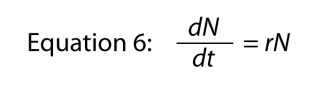
hvor parameteren r er, igen, den indre sats naturlig stigning., Det grundlæggende forhold mellem endelig stigningshastighed og intrinsic rate er
r = ln(R)
hvor ln refererer til den naturlige logaritme. Bemærk at Ligning 6 og Ligning 3 er kun forskellige former af den samme ligning (Ligning 3 er den integrerede form af Ligning 6; Ligning 6 er den differentierede form af Ligning 3), og begge kan betegnes blot som eksponentiel ligning.,

den eksponentielle ligning er en nyttig model af enkle populationer, i det mindste i relativt korte perioder., For eksempel, hvis en laboratorietekniker har brug for at vide, hvornår en bakteriekultur når en bestemt befolkningstæthed, kan den eksponentielle ligning bruges til at give en forudsigelse om nøjagtigt, hvornår denne befolkningsstørrelse nås. Et andet eksempel er i tilfælde af landbrugsskadedyr. Herbivorer er altid potentielt store problemer for planter. Når de planter, der udsættes for sådanne udbrud, er landbrug, det vil sige afgrøder, kan tabet være meget vigtigt for både landmand og forbruger. Der er således altid pres for at forhindre sådanne udbrud., Siden Anden Verdenskrig har det største våben i bekæmpelsen af sådanne skadedyrsudbrud været kemiske pesticider, såsom DDT. Men i de senere år er vi kommet til at indse, at disse pesticider er yderst farlige i det lange løb, både for miljøet og for mennesker. Derfor har der været en bevægelse for at begrænse mængden af pesticider, der sprøjtes for at bekæmpe skadedyr. Den vigtigste måde, dette gøres på, er at etablere en økonomisk tærskel, som er befolkningstætheden af den potentielle skadedyr, under hvilken skaden på afgrøden er ubetydelig (dvs.det er ikke rigtig nødvendigt at sprøjte)., Når skadedyrspopulationen stiger over denne tærskel, skal landbrugeren gribe ind og anvende en slags pesticid eller andre midler til bekæmpelse af skadedyr. I betragtning af arten af dette problem er det undertiden af største betydning at kunne forudsige, hvornår skadedyret når den økonomiske tærskel. At kende R for skadedyrsarterne gør det muligt for landmanden at forudsige, hvornår det bliver nødvendigt at anvende en slags kontrolprocedure (figur 3).
den eksponentielle ligning er også en nyttig model til udvikling af intuitive ideer om populationer., Det klassiske eksempel er en dam med en befolkning af liljepuder. Hvis hver liljepude gengiver sig selv (to puder indtager stedet for, hvor en pude havde været) hver måned, og det tog for eksempel tre år, før dammen blev halvt fyldt med liljepuder, hvor meget længere vil det tage, før dammen er helt dækket med liljepuder? Hvis du ikke holder op med at tænke for klart, er det fristende at sige, at det vil tage lige så lang tid, tre år, for den anden halvdel af dammen at blive så fyldt som den første. Svaret er selvfølgelig en måned.,
et andet populært eksempel er den legendariske gamle egyptiske (eller undertiden persiske) matematiker, der beder betaling fra kongen i form af hvedekorn (undertiden ris). Et korn på den første firkant af et skakbræt, to korn på den anden firkant, og så videre, indtil den sidste firkant. Farao kan ikke forestille sig, at en sådan simpel betaling kunne beløbe sig til meget, og det er enig. Men han værdsatte ikke eksponentiel vækst fuldt ud., Da der er 64 firkanter på skakbrættet, kan vi bruge ligning 2 til at bestemme, hvor mange hvedekorn der skal betales på den sidste firkant (r hævet til den 64.magt, som er omkring 18.446.744.074.000.000.000 — en masse hvede faktisk, bestemt mere end i hele kongeriget). Disse eksempler understreger den ofte overraskende måde, hvorpå en eksponentiel proces kan føre til meget store tal meget hurtigt.
