hurtigt svar:
For en retvinklet trekant:

sinusfunktionen sin tager vinkel and og giver forholdet modsat hypotenuse
den inverse sinusfunktion sin-1 tager forholdet modsatthypotenuse og giver vinkel<
og cosinus og tangent følge en lignende id..,
og nu for detaljerne:
sinus, cosinus og Tangent er alle baseret på en retvinklet trekant
de er meget ens funktioner … så vi vil se på sinusfunktionen og derefter omvendt sinus for at lære, hvad det hele handler om.,
sinusfunktion
Sinusvinklen angle er:
- længden af den modsatte side vinkel divided
- divideret med længden af hypotenusen
eller mere enkelt:
sin(sin) = modsat / hypotenuse
sinusfunktionen kan hjælpe os med at løse ting som dette:
omvendt sinusfunktion
men nogle gange er det den vinkel, vi skal finde.
det er her “Inverse sinus” kommer ind.
det besvarer spørgsmålet “hvilken vinkel har sinus lig med modsat / hypotenuse?,”
symbolet for omvendt sinus er sin-1 eller undertiden arcsin.
De er som frem og tilbage!

- sin tager en vinkel og giver os forholdet “modsat/hypotenuse”
- sin-1 tager forholdet “modsat / hypotenuse” og giver os vinklen.
Eksempel:
Lommeregner
 |
på lommeregneren trykker du på et af følgende (afhængigt af dit mærke af lommeregner):enten ‘2ndF sin’ eller ‘shift sin’. |
på din lommeregner, prøv at bruge sin og derefter sin-1 For at se, hvad der sker
mere end en vinkel!
Inverse sinus viser dig kun en vinkel … men der er flere vinkler, der kunne fungere.
eksempel: her er to vinkler, hvor modsat / hypotenuse = 0.,5
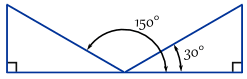
Der er faktisk uendeligt mange vinkler, fordi du kan fortsætte med at tilføje (eller subtrahere) 360!:
husk dette, fordi der er tidspunkter, hvor du faktisk har brug for en af de andre vinkler!
resum And
sinusens vinkel is er:
sin(sin) = modsat / Hypotenuse
og omvendt sinus er :
sin-1 (modsat / Hypotenuse) = =
hvad med “cos” og “tan” … ?
præcis den samme ID., men forskellige sideforhold.,
Cosinus
Cosinus af vinklen θ er:
cos(θ) = Tilstødende / Hypotenusen
Og Invers Cosinus er :
cos-1 (Støder op / Hypotenusen) = θ
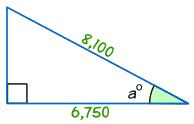
Eksempel: Finde størrelsen af vinkel a°
cos a° = Tilstødende / Hypotenusen
cos a° = 6,750/8,100 = 0.8333…
a = = cos-1 (0, 8333…) = 33.,6 decimal (til 1 decimal)
Tangent
tangenten af vinkel is er:
tan(tan) = modsat / tilstødende
så omvendt Tangent er :
tan-1 (modsat / tilstødende) = <
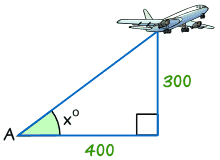
eksempel: find størrelsen på vinkel. <
Tan = = = modsat / tilstødende
tan = = = 300/400 = 0.75
= = = tan-1 (0.75) = 36.,9 decimal (korrekt til 1 decimal)
andre navne
undertiden kaldes sin-1 asin eller arcsin
ligeledes kaldes cos-1 acos eller arccos
og tan-1 kaldes Atan eller arctan
eksempler:
- arcsin(y) er det samme som sin-1(y)
- Atan(Y) er den samme som sin-1(y)
- Atan (y) θ) er det samme som tan-1 (etc)
- osv.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,
- men den Inverse sinus og Inverse cosinus “fortsætter ikke for evigt” som sinus og cosinus gør …
lad os se på eksemplet på cosinus.
Her er Cosinus og Invers Cosinus plottet på samme graf:
Cosinus og Invers Cosinus
De er spejlbilleder (over diagonalen)
Men hvorfor Invers Cosinus få hugget af i top og bund (prikker er egentlig ikke en del af funktionen) … ?
fordi det er en funktion, kan det kun give et svar
, når vi spørger “Hvad er cos-1 (?)?,”
et svar eller uendeligt mange svar
men vi så tidligere, at der er uendeligt mange svar, og den stiplede linje på grafen viser dette.
så ja der er uendeligt mange svar …
… men forestil dig, at du skriver 0.5 i din lommeregner, tryk på cos-1, og det giver dig en uendelig liste over mulige svar …
så vi har denne regel om, at en funktion kun kan give et svar.
så ved at hugge det Sådan får vi kun et svar, men vi skal huske, at der kunne være andre svar.,
Tangent og omvendt Tangent
og her er tangentfunktionen og omvendt tangent. Kan du se, hvordan de er spejlbilleder (om diagonalen) …?

Tangent

omvendt Tangent



