Articles

R-S Squareduared vs justeret r-s ared

februar 2, 2021 februar 2, 2021

efter opbygning af en maskinindlæringsmodel, er det næste trin at evaluere modelydelsen og forstå, hvor god vores model er mod en benchmark-model., Evalueringsmetriken, der skal bruges, afhænger af den type problem, du forsøger at løse —uanset om det er et overvåget eller uovervåget problem, og hvis det er en klassificering eller en regressionsopgave.

i dette indlæg vil jeg tale om to vigtige evalueringsmålinger, der bruges til regressionsproblemer og fremhæve nøgleforskellen mellem dem.

R-kvadreret, også kendt som koefficientbestemmelse, definerer den grad, i hvilken variansen i den afhængige variabel (eller målet) kan forklares med den uafhængige variabel (funktioner).,

lad os forstå dette med et eksempel — siger, at R-S .uared-værdien for en bestemt model kommer ud til at være 0, 7. Dette betyder, at 70% af variationen i den afhængige variabel forklares af de uafhængige variabler.

ideelt set ønsker vi, at de uafhængige variabler er i stand til at forklare al variationen i målvariablen. I dette scenario ville r-s .uared-værdien være 1. Således kan vi sige, at højere R-kvadreret værdi, bedre i modellen.,

så i enkle vendinger, højere R kvadreret, jo mere variation forklares af dine inputvariabler og dermed bedre er din model. Også R-kvadratet vil variere fra 0 til 1. Her er formlen for beregning af R-S squareduared-

R-s squareduared beregnes ved at dividere summen af kvadrater af rester fra regressionsmodellen (givet af SSR ‘ er) med den samlede sum af kvadrater af fejl fra den gennemsnitlige model (givet ved SStot) og derefter trække den fra 1.,

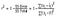
en ulempe ved R-S .uared er, at det antager, at hver variabel hjælper med at forklare variationen i målet, hvilket måske ikke altid er sandt. For eksempel, hvis vi tilføjer nye funktioner til dataene (som måske eller måske ikke er nyttige), vil R-S .uared-værdien for modellen enten stige eller forblive den samme, men den ville aldrig falde.

dette håndteres af en let modificeret version af r-S .uared, kaldet den justerede r-S .uared.,

justeret r-s .uared

i lighed med R-S .uared måler den justerede R-S .uared variationen i den afhængige variabel (eller mål), forklaret af kun de funktioner, der er nyttige til at lave forudsigelser. I modsætning til R-S .uared vil den justerede R-S .uared straffe dig for at tilføje funktioner, som ikke er nyttige til at forudsige målet.

lad os matematisk forstå, hvordan denne funktion er indkvarteret i justeret R-kvadreret., Her er formlen for justeret r-s squareduared

Her r^2 er R-kvadreret beregnet, n er antallet af rækker og M er antallet af kolonner. Når antallet af funktioner stiger, falder værdien i nævneren.

• hvis R2 stiger med en betydelig værdi, vil den justerede R-kvadreret stige.
• hvis der ikke er nogen signifikant ændring i R2, vil den justerede r2 falde.