
I denne artikel, vil du lære om SVM eller Support Vektor Maskine, som er en af de mest populære AI algoritmer (det er en af de top 10 AI algoritmer) og om Kernen Trick, der beskæftiger sig med non-linearitet og højere dimensioner., Vi vil berøre emner som hyperplanes, Lagrange multiplikatorer, vi vil have visuelle eksempler og kodeeksempler (svarende til kodeeksemplet, der bruges i KNN-kapitlet) for bedre at forstå denne meget vigtige algoritme.
SVM forklaret
Support Vector Machine er en overvåget læringsalgoritme, der oftest bruges til klassificering, men den kan også bruges til regression. Hovedid .en er, at algoritmen på baggrund af de mærkede data (træningsdata) forsøger at finde den optimale hyperplan, der kan bruges til at klassificere nye datapunkter. I to dimensioner er hyperplanet en simpel linje.,
normalt forsøger en læringsalgoritme at lære de mest almindelige egenskaber (hvad der adskiller en klasse fra en anden) af en klasse, og klassificeringen er baseret på de repræsentative egenskaber, der læres (så klassificering er baseret på forskelle mellem klasser). SVM arbejder omvendt. Den finder de mest lignende eksempler mellem klasser. Det vil være støttevektorerne.
som et eksempel, lad os overveje to klasser, æbler og citroner.,andre algoritmer lærer de mest tydelige, mest repræsentative egenskaber ved æbler og citroner, ligesom æbler er grønne og afrundede, mens citroner er gule og har elliptisk form.
i modsætning hertil vil SVM søge efter æbler, der ligner meget citroner, for eksempel æbler, der er gule og har elliptisk form. Dette vil være en supportvektor. Den anden støttevektor vil være en citron, der ligner et æble (grønt og afrundet). Så andre algoritmer lærer forskellene, mens SVM lærer ligheder.,
Hvis vi visualisere ovenstående eksempel i 2D, vil vi have noget lignende dette:

Da vi går fra venstre mod højre, alle de eksempler, der vil blive klassificeret som æbler, indtil vi når den gule apple. Fra dette tidspunkt falder tilliden til, at et nyt eksempel er et æble, mens citronklassens tillid øges., Når citronklassens tillid bliver større end æbleklassens tillid, klassificeres de nye eksempler som citroner (et sted mellem det gule æble og den grønne citron).
baseret på disse supportvektorer forsøger algoritmen at finde den bedste hyperplan, der adskiller klasserne. I 2D hyperplane er en linje, så ville det se ud som dette:

Ok, men hvorfor skulle jeg trække den blå grænse, som vist på billedet ovenfor?, Jeg kunne også trække grænser, som denne:

Som du kan se, vi har en uendelig række af muligheder for at trække den beslutning grænse. Så hvordan kan vi finde den optimale?
at finde den optimale Hyperplan
intuitivt er den bedste linje den linje, der er langt væk fra både æble-og citroneksempler (har den største margin)., For at have optimal løsning skal vi maksimere margenen på begge måder (hvis vi har flere klasser, så skal vi maksimere det i betragtning af hver af klasserne).

så hvis vi sammenligner billedet ovenfor med billedet nedenfor, kan vi nemt observere, at den første er den optimale hyperplan (linje) og den anden er en suboptimal løsning, fordi margenen er langt kortere.,

fordi vi ønsker at maksimere margenerne under hensyntagen til alle klasser, i stedet for at bruge en margin for hver klasse, bruger vi en “global” margin, der tager hensyn til alle klasser., Denne margin vil se ud som den lilla linje på følgende billede:

denne margen er ortogonal til grænsen og lige langt til støttevektorerne.
så hvor har vi vektorer? Hver af beregningerne (Beregn afstand og optimale hyperplaner) er lavet i vektorielt rum, så hvert datapunkt betragtes som en vektor. Dimensionen af rummet er defineret af antallet af attributter af eksemplerne., For at forstå matematikken bag, læs venligst denne korte matematiske beskrivelse af vektorer, hyperplanes og optimeringer: SVM kortfattet.
alt i alt er supportvektorer datapunkter, der definerer hyperplanets position og margin. Vi kalder dem” support ” vektorer, fordi disse er de repræsentative datapunkter i klasserne, hvis vi flytter en af dem, ændres positionen og/eller margenen. Flytning af andre datapunkter vil ikke have effekt over marginen eller placeringen af hyperplanet.,
for at lave klassifikationer behøver vi ikke alle træningsdatapunkter (som i tilfældet med KNN), vi skal kun gemme supportvektorerne. I værste fald vil alle punkter være støttevektorer, men det er meget sjældent, og hvis det sker, skal du tjekke din model for fejl eller fejl.
så dybest set er læringen ækvivalent med at finde hyperplanen med den bedste margin, så det er et simpelt optimeringsproblem.,/h2>
De grundlæggende skridt af SVM er:
- vælg to hyperplanes (i 2D), som adskiller de data, der med ingen point mellem dem (røde linjer)
- maksimere deres afstand (margenen)
- den gennemsnitlige linje (her den linje, halvvejs mellem de to røde linjer) vil være den afgørelse grænse
Det er meget godt og nemt, men at finde den bedste margin, optimering problemet er ikke trivielt (det er let i 2D, når vi kun har to attributter, men hvad hvis vi har N dimensioner med N et meget stor antal)
til At løse optimering problem, vi bruger Lagrange Multiplikatorer., For at forstå denne teknik kan du læse følgende to artikler: dualitet Langrange multiplikator og en simpel forklaring på, hvorfor Langrange multiplikatorer Wroks.
indtil nu havde vi lineært adskillelige data, så vi kunne bruge en linje som klassegrænse. Men hvad nu hvis vi skal beskæftige os med ikke-lineære datasæt?,
SVM for Ikke-Lineære Sæt af Data
Et eksempel på ikke-lineære data er:

I dette tilfælde kan vi ikke finde en lige linje til at adskille æbler fra citroner. Så hvordan kan vi løse dette problem. Vi vil bruge kernen Trick!
den grundlæggende id.er, at når et datasæt er uadskilleligt i de nuværende dimensioner, skal du tilføje en anden dimension, måske på den måde kan dataene adskilles., Bare tænk over det, eksemplet ovenfor er i 2D, og det er uadskilleligt, men måske i 3D er der et mellemrum mellem æblerne og citronerne, måske er der en niveauforskel, så citroner er på niveau et og citroner er på niveau to. I dette tilfælde kan vi let tegne en adskillende hyperplan (i 3D er en hyperplan et plan) mellem niveau 1 og 2.
kortlægning til højere dimensioner
for at løse dette problem bør vi ikke bare blindt tilføje en anden dimension, vi bør omdanne rummet, så vi genererer denne niveauforskel med vilje.,
kortlægning fra 2D til 3D
lad os antage, at vi tilføjer en anden dimension kaldet .3. En anden vigtig transformation er, at punkterne i den nye dimension er organiseret ved hjælp af denne formel .12 + .22.
Hvis vi plotter flyet defineret af formula2 + y2-formlen, får vi noget som dette:

nu skal vi kortlægge æblerne og citronerne (som kun er enkle punkter) til dette nye rum. Tænk over det omhyggeligt, hvad gjorde vi?, Vi har lige brugt en transformation, hvor vi tilføjede niveauer baseret på afstand. Hvis du er i oprindelsen, vil punkterne være på det laveste niveau. Når vi bevæger os væk fra oprindelsen, betyder det, at vi klatrer op ad bakken (bevæger os fra midten af flyet mod margenerne), så niveauet af punkterne bliver højere., Hvis vi nu overvejer, at oprindelsen er citronen fra midten, vil vi have noget som dette:
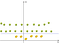
nu kan vi nemt adskille de to klasser. Disse transformationer kaldes kerner. Populære kerner er: polynomisk kerne, Gaussisk kerne, Radial Basisfunktion (RBF), Laplace RBF-kerne, Sigmoid-kerne, Anove RBF-kerne osv. (Se kernefunktioner eller en mere detaljeret beskrivelse af Maskinindlæringskerner).,
Kortlægning fra 1D-2D
en Anden, lettere eksempel i 2D ville være:

Efter at bruge de kerne-og efter alle de forandringer, vi vil få:

Så efter omdannelsen, vi kan sagtens adskille de to klasser ved hjælp af bare en enkelt linje.,
i virkelige applikationer har vi ikke en simpel lige linje, men vi vil have masser af kurver og høje dimensioner. I nogle tilfælde har vi ikke to hyperplaner, der adskiller dataene uden punkter mellem dem, så vi har brug for nogle afvejninger, tolerance for outliers. Heldigvis har SVM-algoritmen en såkaldt regulariseringsparameter til at konfigurere afvejningen og tolerere outliers.
Tuning parametre
som vi så i det foregående afsnit er det afgørende at vælge den rigtige kerne, fordi hvis transformationen er forkert, kan Modellen have meget dårlige resultater., Som en tommelfingerregel skal du altid kontrollere, om du har lineære data, og i så fald skal du altid bruge lineær SVM (lineær kerne). Lineær SVM er en parametrisk model, men en RBF-kerne SVM er det ikke, så kompleksiteten af sidstnævnte vokser med størrelsen på træningssættet. Ikke kun er dyrere at træne en RBF-kerne SVM, men du er også nødt til at holde kernematri .en rundt, og projektionen i dette “uendelige” højere dimensionelle rum, hvor dataene bliver lineært adskillelige, er også dyrere under forudsigelse., Desuden har du flere hyperparametre at tune, så modelvalg er også dyrere! Og endelig er det meget nemmere at overfede en kompleks model!
regularisering
Regulariseringsparameteren (i python hedder det C) fortæller SVM-optimeringen, hvor meget du vil undgå miss klassificere hvert træningseksempel.
Hvis C er højere, vil optimeringen vælge mindre margin hyperplan, så træningsdata miss klassifikation sats vil være lavere.,
På den anden side, hvis C er lav, vil margenen være stor, selvom der vil være miss classified training data eksempler. Dette er vist i følgende to diagrammer:

som du kan se på billedet, når c er lav, er margenen højere (så implicit har vi ikke så mange kurver, linjen følger ikke strengt datapunkterne), selvom to æbler blev klassificeret som citroner., Når C er høj, er grænsen fuld af kurver, og alle træningsdata blev klassificeret korrekt. Glem ikke, selvom alle træningsdata var korrekt klassificeret, betyder det ikke, at forøgelse af C altid vil øge præcisionen (på grund af overfitting).
Gamma
Den næste vigtige parameter er Gamma. Gamma-parameteren definerer, hvor langt indflydelsen af et enkelt træningseksempel når. Det betyder, at høj Gamma kun vil overveje punkter tæt på den plausible hyperplan og lav Gamma vil overveje punkter på større afstand.,

som du kan se, vil reduktion af gamma resultere i, at finde den korrekte hyperplan vil overveje punkter på større afstande, så flere og flere punkter vil blive brugt (grønne linjer angiver, hvilke punkter der blev overvejet, når man finder den optimale hyperplan).
Margin
den sidste parameter er marginen. Vi har allerede talt om margin, højere margin resultater bedre model, så bedre klassificering (eller forudsigelse)., Margenen skal altid maksimeres.
SVM eksempel ved hjælp af Python
i dette eksempel vil vi bruge Social_net .orks_ads.csv-fil, den samme fil som vi brugte i den foregående artikel, se KNN eksempel ved hjælp af Python.
i dette eksempel vil jeg kun skrive ned forskellene mellem SVM og KNN, fordi jeg ikke vil gentage mig selv i hver artikel! Hvis du vil have hele forklaringen om, hvordan kan vi læse datasættet, hvordan analyserer og opdeler vi vores data, eller hvordan kan vi evaluere eller plotte beslutningsgrænserne, så læs venligst kodeeksemplet fra det forrige kapitel (KNN)!,da sklearn-biblioteket er et meget velskrevet og nyttigt Python-bibliotek, har vi ikke for meget kode til at ændre. Den eneste forskel er, at vi skal importere SVC-klassen (SVC = SVM i sklearn) fra sklearn.svm i stedet for KNeighborsClassifier klasse fra sklearn.nabo.
efter import af SVC kan vi oprette vores nye model ved hjælp af den foruddefinerede konstruktør. Denne konstruktør har mange parametre, men jeg vil kun beskrive de vigtigste, det meste af tiden bruger du ikke andre parametre.,
de vigtigste parametre er:
- kernel: den kernetype, der skal bruges. De mest almindelige kerner er rbf (dette er standardværdien), poly eller sigmoid, men du kan også oprette din egen kerne.,
- C: det er normaliserede parameter, der er beskrevet i Tuning Parametre punkt
- gamma: dette blev også beskrevet i Tuning Parametre punkt
- grad: det er kun anvendes, hvis den valgte kerne er poly og sæt den grad af polinom
- sandsynlighed: dette er en boolesk parameter, og hvis det er sandt, så er modellen vil vende tilbage for hver forudsigelse, vektor af sandsynligheden for at tilhøre hver klasse af responsvariabel. Så dybest set vil det give dig fortrolighederne for hver forudsigelse.,
- krympning: dette viser, om du vil have en krympende heuristisk brugt i din optimering af SVM, som bruges i sekventiel Minimal optimering. Det er standardværdien er sand, en hvis du ikke har en god grund, skal du ikke ændre denne værdi til falsk, fordi krympning i høj grad vil forbedre din ydeevne, for meget lidt tab med hensyn til nøjagtighed i de fleste tilfælde.
lad os nu se output for at køre denne kode., Beslutningsgrænsen for træningssættet ser sådan ud:

som vi kan se, og som vi har lært i afsnittet indstillingsparametre, fordi C har en lille værdi (0.1) er beslutningsgrænsen glat.
nu, hvis vi øger C fra 0.,1 til 100, som vi vil have flere kurver i afgørelsen grænse:

Hvad ville der ske, hvis vi bruger C=0.1 men nu er vi øge Gamma fra 0,1 til 10? Lad os se!

Hvad skete der her? Hvorfor har vi sådan en dårlig model?, Som du har set i afsnittet indstillingsparametre betyder høj gamma, at når vi beregner den plausible hyperplan, betragter vi kun punkter, der er tætte. Nu fordi tætheden af de grønne punkter kun er høj i den valgte grønne region, er punkterne tæt nok på den plausible hyperplan, så disse hyperplaner blev valgt. Vær forsigtig med gamma-parameteren, fordi dette kan have en meget dårlig indflydelse på resultaterne af din model, hvis du indstiller den til en meget høj værdi (hvad der er en “meget høj værdi” afhænger af datapunktets tæthed).,
i dette eksempel er de bedste værdier for C og Gamma 1,0 og 1,0. Hvis vi nu kører vores model på testsættet, får vi følgende diagram:

og forvirringsmatri theen ser sådan ud:

som du kan se, har vi kun 3 falske positiver og kun 4 falske negativer., Nøjagtigheden af denne model er 93% , hvilket er et rigtig godt resultat, vi opnåede en bedre score end at bruge KNN (som havde en nøjagtighed på 80%).
Bemærk: nøjagtighed er ikke den eneste metrisk, der bruges i ML, og heller ikke den bedste metrisk til at evaluere en model på grund af Nøjagtighedsparadokset. Vi bruger denne metrik til enkelhed, men senere i kapitelmetrikkerne til evaluering af AI-algoritmer vil vi tale om Nøjagtighedsparadokset, og jeg vil vise andre meget populære målinger, der bruges i dette felt.,
konklusioner
i denne artikel har vi set en meget populær og kraftfuld overvåget læringsalgoritme, Support Vector Machine. Vi har lært den grundlæggende id., hvad er en hyperplan, hvad er støttevektorer og hvorfor er de så vigtige. Vi har også set masser af visuelle repræsentationer, som hjalp os til bedre at forstå alle begreberne.et andet vigtigt emne, som vi rørte ved, er Kernetricket, som hjalp os med at løse ikke-lineære problemer.
for at få en bedre model så vi teknikker til at indstille algoritmen., I slutningen af artiklen havde vi et kodeeksempel i Python, som viste os, hvordan vi kan bruge KNN-algoritmen.
som endelige tanker vil jeg gerne give nogle fordele & ulemper og nogle populære brugssager.,
fordele
- SVN kan være meget effektiv, fordi den kun bruger en delmængde af træningsdataene, kun supportvektorerne
- fungerer meget godt på mindre datasæt, på ikke-lineære datasæt og høje dimensionelle rum
- er meget effektiv i tilfælde, hvor antallet af dimensioner er større end antallet af prøver
- det kan have høj nøjagtighed, nogle gange kan det fungere endnu bedre end neurale netværk
- ikke meget følsomt over for overfitting
ulemper
- træningstiden er høj, når vi har store datasæt
- , når datasættet har mere støj (i.,e. mål klasser er overlappende) SVM ikke udføre
en Populær Use Cases
- Sms-Klassifikation
- registrering af spam
- Sentiment analyse
- Aspekt-baseret anerkendelse
- Aspekt-baseret anerkendelse
- Håndskrevne ciffer anerkendelse
