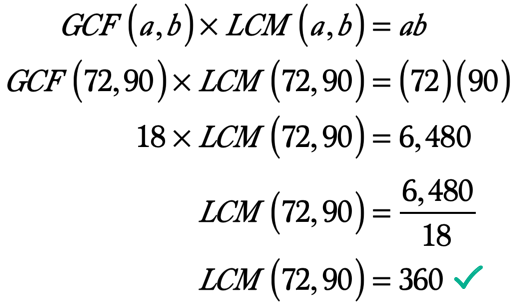Als Sie studierten, wie man den GCF und LCM von zwei positiven Zahlen findet, haben Sie eine sehr interessante Beziehung zwischen den beiden Mengen entdeckt?

ich Tat! Ich habe es tatsächlich zufällig entdeckt, als ich ein junger Student war, und ich dachte, ich stolperte über etwas, das „revolutionär“war. Ich war so aufgeregt, dass ich es mit meinem Lehrer teilte., Aber zu meiner Frustration sah er mir in die Augen und sagte, dass es bereits eine bewährte mathematische Aussage sei. Ich fühlte mich für einen Moment entmutigt, aber ich ging zurück zu meiner Schularbeit und drückte weiter.

Wenn Sie noch nicht darauf gestoßen sind, besteht eine bemerkenswerte algebraische Beziehung oder Verbindung zwischen dem größten gemeinsamen Faktor (GCF) und dem kleinsten gemeinsamen Vielfachen (LCM) zweier Zahlen. In dieser Lektion sind die Zahlen, die wir wollen, diejenigen, die nur zur Menge positiver Ganzzahlen gehören.,
Unten ist die algebraische Verbindung zwischen dem GCF und dem LCM von zwei positiven ganzen Zahlen.
Die GCF-LCM-Formel
WARNUNG: Es gibt wirklich keine“GCF-LCM-Formel“. Ich habe gerade den Namen für eine einfache Referenz. Sie können es alles nennen, was Sie wollen, solange es seinen Zweck erfüllt.,
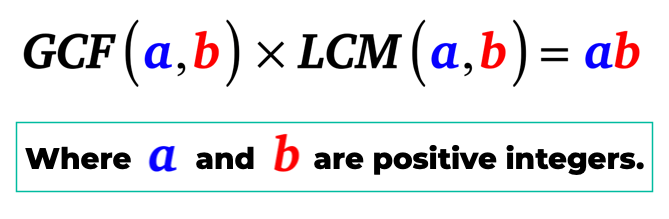
Einfach ausgedrückt ist der größte gemeinsame Faktor von a und b, wenn er mit dem kleinsten gemeinsamen Vielfachen von a und b multipliziert wird, gleich zum Produkt von a und b. Das heißt, a und b sind positive ganze Zahlen.
Beispielprobleme
Beispiel 1: Der GCF von 12 und 16 ist 4. Was ist das LCM von 12 und 16?
Sie können die LCM von 12 und 16 mit einer der beiden folgenden Methoden bestimmen.,
- LCM mit der Listenmethode
- LCM mit der Primfaktorisierungsmethode
finden Es gibt jedoch einen viel schnelleren Weg. Sie können die „GCF-LCM-Formel“ nutzen, da Sie die beiden Ganzzahlen und deren GCF kennen. Stecken Sie einfach die Werte in die Formel und lösen Sie sie für das LCM.
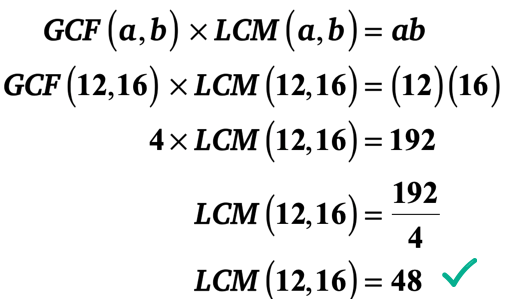
Ich überlasse es Ihnen zu überprüfen, ob das LCM von 12 und 16 tatsächlich 48 ist.
Beispiel 2: Das LCM von 24 und 40 ist 120. Was ist der GCF von 24 und 40?,
Dieses Problem ist das genaue Gegenteil von Beispiel 1, da Sie den Wert des LCM anstelle von GCF erhalten.
Das sind also die Informationen, die wir kennen. Lassen Sie uns sie zur Klarheit auflisten.
▶︎ LCM (24,40) = 120
▶︎ a=24 und b=40 daher ab = \left ({24} \right)\left ({40} \right) = 960
📌 Hinweis: Es spielt keine Rolle, welche Zahlen a und b sind. Es ist jedoch eine gute Praxis, Ihre Lösung zu standardisieren. Ich schlage vor, dass Sie a die kleinere Ganzzahl sein lassen, während b die größere Ganzzahl ist.,
Setzen wir die bekannten Werte in die Formel ein und lösen Sie dann für den GCF von 24 und 40.
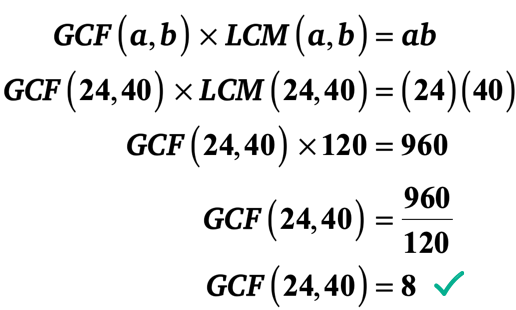
Beispiel 3: Ermitteln Sie den GCF von 20 und 25, indem Sie zuerst das LCM von 20 und 25 berechnen.
Dieses Problem unterscheidet sich etwas von den Beispielen #1 und #2. Sie müssen zuerst das Least Common Multiple (LCM) von 20 und 25 berechnen. Danach können Sie den größten gemeinsamen Faktor (GCF) von 20 und 25 mithilfe der GCF-LCM-Formel lösen.
Also los geht ‚ s!, Um das LCM von 20 und 25 zu finden, schreiben wir die ersten paar Vielfachen von 20 und 25. Das allererste gemeinsame Vielfache, das auftaucht, wird unser LCM sein.
Vielfache von 20: 20, 40, 60, 80, 100, 120
Vielfache von 25: 25, 50, 75, 100, 125, 150
Da die Zahl 100 als erstes gemeinsames Vielfaches von 20 und 25 angezeigt wird, können wir behaupten, dass das LCM von 20 und 25 100 ist.
Wir haben jetzt alle Informationen, um die Formel zu verwenden. Nachfolgend sind die Werte aufgeführt, die wir in die zu lösende Formel für das LCM von 20 und 25 einfügen werden.,
◉ Das Produkt von a und b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ Das LCM von 20 und 25 → LCM\left( {20,25} \right) = 100
Hier ist die Berechnung für den GCF von 20 und 25:
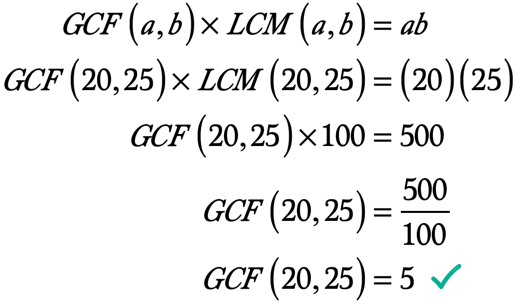
Beispiel 4: Suchen Sie das LCM von 63 und 84, indem Sie zuerst den GCF von 63 und 84 berechnen.
Dieses Problem ist dem Beispiel #3 sehr ähnlich. Der einzige Unterschied besteht darin, dass Sie zuerst den GCF anstelle des LCM berechnen, wie vom Problem selbst angewiesen.,
Lassen Sie uns alle Faktoren von 63 und 84 finden. Sie können die“ Rainbow method “ – Technik verwenden, um die angegebenen Ganzzahlen zu berücksichtigen.
Beachten Sie, dass der größte oder höchste gemeinsame Faktor zwischen den beiden Listen 21 ist.
63: 1, 3, 7, 9, 21, 63
Faktoren von 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Daher ist der größte gemeinsame Faktor von 63 und 84 21. So, GCF\left( {63,84} \right) = 21.,
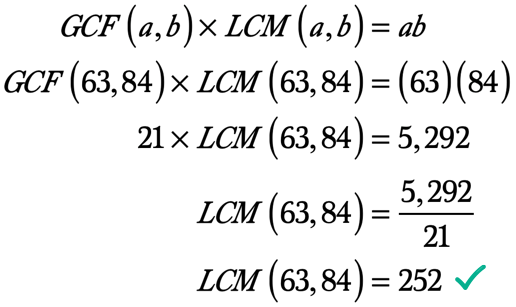
Beispiel 5: hier Finden Sie das LCM von 72 und 90 über die GCF-und LCM-Formel.
Wie wir bereits wissen, können wir das LCM von zwei ganzen Zahlen mit dem Wert seines GCF mithilfe der GCF-LCM-Formel finden.,
Auflistung der Faktoren 72 und 90, wir haben:
Alle Faktoren von 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Alle Faktoren von 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Wenn wir die Faktorlisten vergleichen, sehen wir, dass 18 der Faktor ist, der beiden gemeinsam ist, aber den größten oder größten Wert hat. Es bedeutet, dass der GCF von 72 und 90 18 ist, dh GCF\left( {72,90} \right) = 18.
Wir sind jetzt bereit, die folgenden Werte in der Formel zu ersetzen.,
❖ ab = \ left ({72} \right)\left ({90} \right) = 6,480
❖ GCF\left ({72,90} \right) = 18
Hier ist die Berechnung, um das LCM zu finden, da wir bereits den GCF der beiden ganzen Zahlen und ihres Produkts kennen.