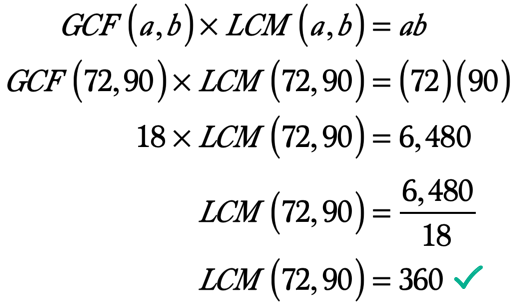Kun tutkit, miten löytää GCF ja LCM kaksi positiivista numerot, saitko selville erittäin mielenkiintoinen suhde kahden määriä?

tein! Huomasin sen sattumalta, kun olin nuori opiskelija ja luulin törmänneeni johonkin, joka oli ”vallankumouksellinen”. Olin niin innoissani, että kerroin siitä opettajalleni., Mutta minun turhautumista, hän katsoi minua silmiin ja sanoi, että se oli jo todistettu matemaattinen selvitys. Olin hetken lannistunut, mutta palasin takaisin koulutyöhöni ja painoin eteenpäin.

Jos et ole kohdannut sitä, on merkittävä algebrallinen suhde tai yhteys Suurin Yhteinen Tekijä (GCF) ja pienin Yhteinen jaettava (LCM) ja kaksi numeroa. Tässä oppitunnissa, numerot, että haluamme ovat ne kuuluvat joukko positiivisia kokonaislukuja vain.,
alla on algebrallinen yhteys GCF: n ja kahden positiivisen kokonaisluvun LCM: n välillä.
GCF-LCM Kaava
VAROITUS: ei ole sellaista asiaa kuin ”GCF-LCM Kaava”. Keksin nimen viittauksen helpottamiseksi. Voit kutsua sitä miksi haluat, kunhan se palvelee tarkoitustaan.,
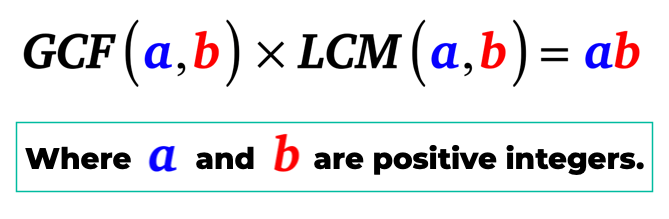
Yksinkertaisesti sanottuna, suurin yhteinen tekijä a ja b, kun kerrotaan pienin yhteinen jaettava a ja b on yhtä suuri kuin tuotteen a ja b. Eli a ja b ovat positiivisia kokonaislukuja.
Esimerkki Ongelmia,
Esimerkki 1: GCF 12 ja 16 on 4. Mikä on LCM 12 ja 16?
voit määrittää 12 ja 16 kohdan LCM: n jommallakummalla seuraavista menetelmistä.,
- Löytää LCM-käyttämällä Luettelo-Menetelmä
- Löytää LCM käyttäen Prime Factorization Menetelmä
Kuitenkin, on paljon nopeampi tapa. Voit hyödyntää ”GCF-LCM-Kaava”, koska tiedät kaksi kokonaislukua ja sen GCF. Kytke arvot kaavaan ja ratkaise LCM: lle.
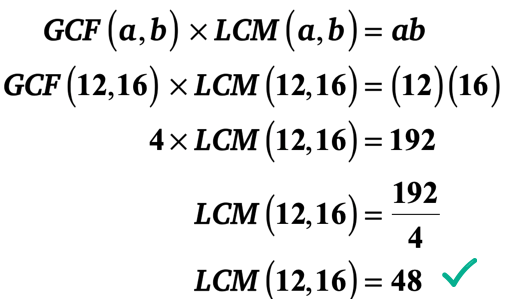
jätän sen sinulle tarkistaa, että LCM 12 ja 16 on todellakin 48.
Esimerkki 2: 24: n ja 40: n LCM on 120. Mikä on GCF 24 ja 40?,
tämä ongelma on täsmälleen päinvastainen kuin esimerkki 1, Koska sinulle annetaan LCM: n arvo GCF: n sijaan.
joten nämä ovat ne tiedot, jotka tiedämme. Tehdään niistä selvyys.
▶︎ LCM(24,40) = 120
▶︎ a=24 ja b=40 siis ab = \left( {24} \right)\left( {40} \right) = 960
📌 Huomautus: Se ei ole oikeastaan väliä, mitkä numerot ovat a ja b. Se ei muuta lopputulosta lopullinen vastaus. On kuitenkin hyvä käytäntö standardoida ratkaisu. Ehdotan, että annat a on pienempi kokonaisluku, kun taas b on suurempi kokonaisluku.,
vaihdetaan tunnetut arvot formula_24 ja 40 välille GCF.
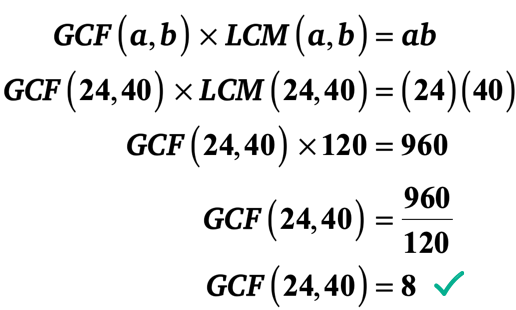
Esimerkki 3: Etsi GCF 20 ja 25 laskemalla ensin LCM 20 ja 25.
tämä ongelma poikkeaa hieman esimerkeistä #1 ja #2. Sinun täytyy laskea ensin vähiten yhteinen Multiple (LCM) 20 ja 25. Sen jälkeen, voit ratkaista Suurin Yhteinen Tekijä (GCF), 20 ja 25 käyttämällä GCF-LCM-Kaava.
so here we go!, Löytää LCM 20 ja 25, me kirjoittaa muutaman ensimmäisen kerrannaisia 20 ja 25. Ensimmäinen yhteinen moninkertainen, joka ilmestyy on meidän LCM.
Kerrannaisia 20: 20, 40, 60, 80, 100, 120
Kerrannaisia 25: 25, 50, 75, 100, 125, 150
Koska numero 100 ilmestyy ensimmäinen yhteinen jaettava 20 ja 25, sitten voimme väittää, että LCM 20 ja 25 on 100.
meillä on nyt kaikki tiedot kaavan käyttöön. Alla on arvot, jotka aiomme korvata kaavan ratkaista LCM 20 ja 25.,
◉ tuote-ja b – → ab = \left( {20} \right)\left( {25} \right) = 500
◉ LCM 20 ja 25 → LCM\left( {20,25} \right) = 100
Tässä on laskelma ratkaista GCF 20 ja 25:
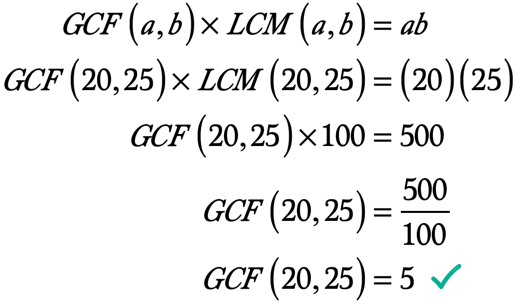
Esimerkki 4: Löytää LCM 63 ja 84 laskemalla ensin GCF 63 ja 84.
tämä ongelma on hyvin samankaltainen kuin esimerkki #3. Ainoa ero on, että lasket ensin GCF sijasta LCM, ohjeiden mukaan ongelma itse.,
Let ’ s find all the factors of 63 and 84. Voit käyttää” rainbow method ” – tekniikkaa laskea annetut kokonaisluvut.
huomaa, että suurin tai korkein yhteinen tekijä näiden kahden luettelon välillä on 21.
Tekijät 63: 1, 3, 7, 9, 21, 63
Tekijät 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
näin Ollen, Suurin Yhteinen Tekijä, 63 ja 84 on 21. Näin ollen GCF\left ({63,84} \right) = 21.,
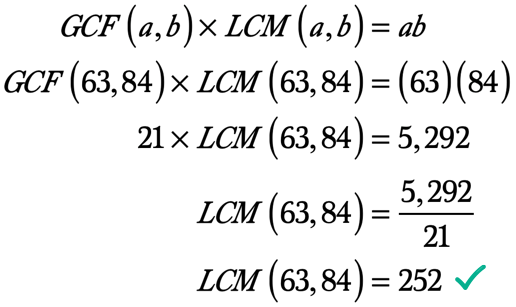
Esimerkki 5: Löytää LCM 72 ja 90 käyttää GCF-LCM-Kaava.
kuten jo tiedämme, voimme löytää kahden kokonaisluvun LCM: n, jonka arvo on sen GCF käyttäen GCF-LCM-kaavaa.,
Listaus sekä tekijöitä, 72 ja 90, meillä on:
Kaikki tekijät 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Kaikki tekijät 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Kun vertaamme luetellaan tekijöitä, voimme nähdä, että 18 on tekijä, joka on yhteinen molemmille, mutta on suurin tai suurin arvo. Se tarkoittaa, että 72 ja 90: n GCF on 18 eli GCF\left( {72,90} \right) = 18.
olemme nyt valmiita korvaamaan alla olevat arvot kaavassa.,
❖ ab = \left( {72} \right)\left( {90} \right) = 6,480
❖ GCF\left( {72,90} \right) = 18
Tässä on laskelma löytää LCM koska tiedämme jo, että GCF kaksi kokonaislukua ja niiden tuote.