A maneira mais fácil de capturar a ideia de uma crescente população com um único organismo unicelular, como uma bactéria ou um cilliate. Na Figura 1, uma população de paramécio em uma pequena depressão de laboratório é retratada. Nesta população os indivíduos dividem-se uma vez por dia. Então, começando com um único indivíduo no dia 0, esperamos, em dias sucessivos, 2, 4, 8, 16, 32, e 64 indivíduos na população., Podemos ver aqui que, em qualquer dia em particular, o número de indivíduos na população é simplesmente o dobro do que o número foi o dia anterior, de modo que o número de hoje, chamá-lo de N(hoje), é igual a duas vezes o número de ontem, chamá-lo de N(ontem), que podemos escrever de forma mais compacta como N(hoje) = 2N(ontem).
então faz sentido escrever isto como, N(t) = 2N(t – 1) onde T poderia assumir qualquer valor em tudo.,
Agora podemos generalizar esta ideia um pouco se nota-se que no dia seis o número é igual a duas vezes o número no dia cinco, ou N(6) = 2N(5) e no dia cinco o número é igual a duas vezes o número no dia quatro, ou N(5) = 2N(4), etc.
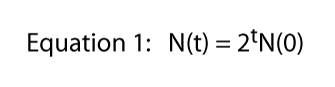
, onde t representa a qualquer hora (por exemplo, se t = 6, N(6) = 26).
finalmente notamos que esta equação foi derivada da situação específica mostrada na Figura 1, onde uma divisão por dia era a regra dura e rápida., É daí que vem o 2 na equação 1 — de cada paramécio individual obtemos dois indivíduos no dia seguinte. Claro que a taxa de divisão pode ser qualquer coisa. Se houvesse duas divisões por dia, mas uma célula sempre morria, esperaríamos três indivíduos de cada indivíduo e a equação 1 seria N(t) = 3tN(0)., Assim, a divisão de taxa pode ser qualquer número e a equação geral torna-se,
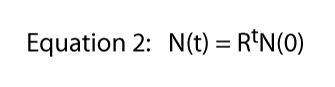
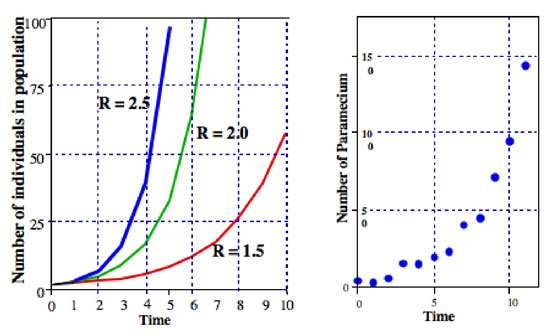
, onde R é normalmente chamado de taxa finita de aumento populacional (em reais caso de desdobramento de Paramecium taxa finita de aumento populacional é igual à divisão de taxa). Na Figura 2 ilustramos esta equação para vários valores de R. é normalmente referido como a equação exponencial, e a forma dos dados na Figura 2 é a forma geral chamado de exponencial.,
o valor de R pode ser representado em um número infinito de formas (por exemplo, se R = 16, podemos escrever R = 8 x 2, ou R = 42, ou R = 32/2, ou R = 2.718282.77). Esta última expressão (R = 2.718282.,77) faz uso de uma constante importante que pode ser lembrada do cálculo elementar, constante de Euler. Expressar qualquer valor de R como constante de Euler elevada a algum poder é realmente extremamente útil-ele traz o poder total do cálculo para a imagem.,olize de Euler constante e podemos escrever a Equação 2 como
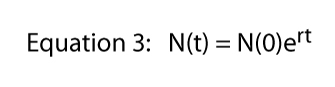
Agora, se tomarmos o logaritmo natural de ambos os lados da Equação 3 — lembre-se ln(ex) = x — Equação 3 torna-se: ln = ln + rt
E se começamos a população com um único indivíduo (como no exemplo acima), temos

a partir do qual podemos ver que o log natural da população, em um determinado momento, algumas constante, vezes esse tempo., A constante r é referida como a taxa intrínseca de aumento natural (Figura 2).
Todos os tipos de microorganismos exibem padrões que estão muito perto do crescimento exponencial da população. Por exemplo, no gráfico da mão direita da Figura 2 está uma população de paramécio crescendo em uma cultura de laboratório. O padrão de crescimento é muito próximo do padrão da equação exponencial.
outra forma de escrever a equação exponencial é como uma equação diferencial, isto é, representando o crescimento da população em sua forma dinâmica., Ao invés de se perguntar qual é o tamanho da população no tempo t, podemos perguntar, o que é a taxa em que a população está a crescer no tempo t. A taxa é simbolizado como o dN/dt, que significa simplesmente “mudar de N em relação à alteração no t,” e se você se lembrar de base de cálculo, podemos encontrar a taxa de crescimento através da diferenciação da Equação 4, o que nos dá
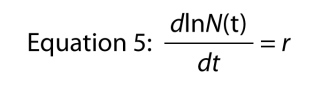
o que é uma coisa extraordinária, porque ele diz que a taxa de crescimento do log do número na população é constante., Essa taxa constante de crescimento do log da população é a taxa intrínseca de aumento.,
Lembrar que a taxa de variação do log de um número é o mesmo que o “per capita” mudança nesse número, o que significa que podemos escrever a Equação 5, como

, onde podemos omitir a variável t, pois é óbvio para onde vai, e então nós reorganizar um pouco para vir acima com
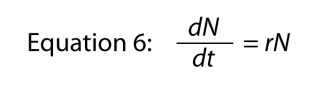
onde o parâmetro r é, novamente, a taxa intrínseca de aumento natural., A relação básica entre a taxa de aumento finita e a taxa intrínseca é
r = ln(R)
Onde ln se refere ao logaritmo natural. Note que a Equação 6 e a Equação 3, são apenas formas diferentes de uma mesma equação (Equação 3 é a forma integrada da Equação 6; Equação 6 é a diferenciada forma de Equação 3), e ambas podem ser referido simplesmente como a equação exponencial.,

A equação exponencial é um modelo útil de simples populações, pelo menos por períodos de tempo relativamente curtos., Por exemplo, se um técnico de laboratório precisa saber quando uma cultura bacteriana atinge uma certa densidade populacional, a equação exponencial pode ser usada para fornecer uma previsão de exatamente quando o tamanho da população será atingido. Outro exemplo é o caso das pragas agrícolas. Os herbívoros são sempre problemas potencialmente importantes para as plantas. Quando as plantas sujeitas a tais surtos são agrícolas, ou seja, culturas, a perda pode ser muito significativa tanto para o agricultor como para o consumidor. Assim, há sempre pressão para evitar tais surtos., Desde a Segunda Guerra Mundial, a principal arma na luta contra esses surtos de pragas tem sido pesticidas químicos, como o DDT. No entanto, nos últimos anos, apercebemo-nos de que estes pesticidas são extremamente perigosos a longo prazo, tanto para o ambiente como para as pessoas. Consequentemente, tem havido um movimento para limitar a quantidade de pesticidas que são pulverizados para combater pragas. A principal forma de fazer isso é estabelecer um limiar econômico, que é a densidade populacional da praga potencial abaixo da qual os danos à cultura é insignificante (ou seja, não é realmente necessário pulverizar)., Quando a população de pragas aumenta acima desse limiar, o agricultor precisa tomar medidas e aplicar algum tipo de pesticida, ou outros meios de controlar a praga. Dada a natureza deste problema, é por vezes da maior importância poder prever quando é que a peste atingirá o limiar económico. O conhecimento do R para as espécies de pragas permite ao agricultor prever quando será necessário aplicar algum tipo de procedimento de controlo (Figura 3). a equação exponencial também é um modelo útil para desenvolver ideias intuitivas sobre populações., O exemplo clássico é um lago com uma população de lírio. Se cada lírio se reproduz a si próprio (duas almofadas ocupam o lugar de onde um lírio tinha estado) a cada mês, e levou, digamos, três anos para que o lago se tornasse meio cheio de lírio pads, quanto mais tempo demorará para que o lago seja completamente coberto de lírio pads? Se você não parar para pensar muito claramente, é tentador dizer que levará tanto tempo, três anos, para que a segunda metade do lago se torne tão cheia quanto a primeira. A resposta, é claro, é um mês., outro exemplo popular é o proverbial matemático egípcio (ou às vezes persa) que pede o pagamento do rei na forma de grãos de trigo (às vezes arroz). Um grão na primeira praça de um tabuleiro de xadrez, dois grãos na segunda praça, e assim por diante, até a última Praça. O Faraó não pode imaginar que um pagamento tão simples poderia ser muito, e assim concorda. Mas ele não apreciou totalmente o crescimento exponencial., Uma vez que existem 64 quadrados no tabuleiro de xadrez, podemos usar a equação 2 para determinar quantos grãos de trigo serão necessários para pagar no último quadrado (R elevado à 64ª potência, que é cerca de 18.446.744.074.000.000 — um monte de trigo, certamente mais do que em todo o Reino). Estes exemplos enfatizam a forma frequentemente surpreendente em que um processo exponencial pode levar a números muito grandes muito rapidamente.
