Resposta Rápida:
Para a direita, triângulo rectângulo:

A função seno pecado leva o ângulo θ e dá a relação oposto hipotenusa
A inversa da função seno sin-1 leva a proporção oppositehypotenuse e dá o ângulo θ
E o co-seno e tangente de seguir uma ideia semelhante.,
e agora para os detalhes:
seno, cosseno e tangente são todos baseados em um triângulo de ângulo direito
são funções muito semelhantes … então vamos olhar para a função Sine e, em seguida, inverter Sine para aprender o que é tudo sobre.,
Função Seno
O Seno do ângulo θ é:
- o comprimento do lado Oposto ao ângulo θ
- dividida pelo comprimento da Hipotenusa
Ou, mais simplesmente:
sin(θ) = Oposto / Hipotenusa
A Função Seno pode ajudar-nos a resolver as coisas como esta:
Inversa da Função Seno
Mas às vezes é o ângulo precisamos encontrar.
é aqui que entra” seno inverso”. ele responde à pergunta ” que ângulo tem seno igual a oposto / hipotenusa?,”
O símbolo para seno inverso é sin-1, ou às vezes arcsin.
eles são como para a frente e para trás!

- o pecado leva um ângulo e dá-nos a razão oposto/hipotenusa”
- sin-1 leva a razão oposto/hipotenusa” e nos dá o ângulo.
exemplo:
Calculadora
 |
Na calculadora você pressione uma das seguintes opções (dependendo da sua marca de calculadora):o ‘2ndF pecado’ ou ‘shift pecado’. |
na sua calculadora, tente usar o sin e depois o sin-1 para ver o que acontece
mais de um ângulo!
seno inverso só lhe mostra um ângulo … mas há mais ângulos que podem funcionar.
exemplo: aqui estão dois ângulos onde oposto / hipotenusa = 0.,5
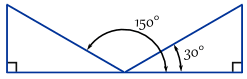
Na verdade, há um número infinito de ângulos, porque você pode continuar adicionando (ou subtraindo) 360°:
Lembre-se que este, porque há momentos em que você realmente precisa de um dos outros ângulos!
Resumo
O Seno do ângulo θ é:
sin(θ) = Oposto / Hipotenusa
E o Inverso do Seno é :
sin-1 (Oposto / Hipotenusa) = θ
Sobre o Que “cos” e “tan” … ?
exactamente a mesma ideia, mas relações laterais diferentes.,
co-seno
O co-seno do ângulo θ é:
cos(θ) = Adjacente / Hipotenusa
E co-seno Inverso é :
cos-1 (Adjacente / Hipotenusa) = θ
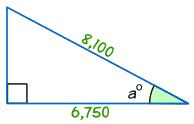
Exemplo: Encontrar o tamanho de um ângulo°
cos a° = Adjacente / Hipotenusa
cos a° = de 6.750/8,100 = 0.8333…
a° = cos-1 (0,8333…) = 33.,6° (para 1 casa decimal)
Tangente
A Tangente do ângulo θ é:
tan(θ) = Oposto / Adjacentes
de Modo Inverso da Tangente é :
tan-1 (Oposto / Adjacentes) = θ
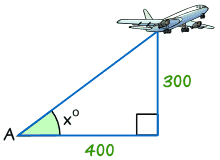
Exemplo: Encontrar o tamanho do ângulo x°
tan x° = Oposto / Adjacentes
tan x° = 300/400 = 0.75
x° = tan-1 (0.75) = 36.,9° (correta para 1 casa decimal)
Outros Nomes
algumas Vezes pecam-1 é chamado de asin ou arcsin
da Mesma forma, cos-1 é chamado de acos ou arccos
E tan-1 é chamado atan ou arctan
Exemplos:
- arcsin(y) é o mesmo que pecado-1(y)
- atan(θ) é o mesmo que tan-1(θ)
- , etc.,
The Graphs
And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine:

Sine

Inverse Sine

Cosine

Inverse Cosine
Did you notice anything about the graphs?
- They look similar somehow, right?,mas o seno inverso e o cosseno inverso não” vão para sempre ” como o seno e o coseno …
vejamos o exemplo do cosseno.
aqui está cosseno e cosseno inverso plotados no mesmo grafo:
cosseno e cosseno inverso
são imagens espelho (sobre a diagonal)
mas porque é que o cosseno inverso é cortado em cima e em baixo (os pontos não fazem realmente parte da função) … ?
porque para ser uma função só pode dar uma resposta
quando perguntamos ” o que é cos-1(x) ?,”
uma resposta ou infinitamente muitas respostas
mas vimos anteriormente que existem infinitamente muitas respostas, e a linha pontilhada no gráfico mostra isto.então sim, há infinitamente muitas respostas …
… mas imagine que você digite 0.5 em sua calculadora, pressione cos – 1 e ele lhe dá uma lista interminável de possíveis respostas …
então temos esta regra de que uma função só pode dar uma resposta.então, cortando-o assim, obtemos apenas uma resposta, mas devemos lembrar-nos que pode haver outras respostas.,
tangente e tangente inversa
e aqui está a função tangente e tangente inversa. Você pode ver como eles são imagens espelho (sobre a diagonal) …?

Tangente

Inversa da Tangente



