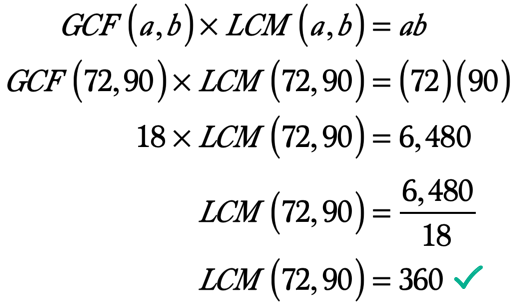quando estava a estudar como encontrar o GCF e o LCM de dois números positivos, descobriu uma relação muito interessante entre as duas quantidades?

eu fiz! Descobri-o por acidente quando era jovem e pensei ter tropeçado em algo que era “revolucionário”. Estava tão entusiasmado que o partilhei com o meu professor., Mas para minha frustração, ele me olhou nos olhos e disse que já era uma afirmação matemática comprovada. Senti-me desanimado por um momento, mas voltei para o trabalho da escola e continuei.

Se você ainda não encontrou ainda, há uma notável algébrica de relação ou vínculo entre o Maior Fator Comum (GCF) e o Mínimo Múltiplo Comum (MMC) de dois números. Nesta lição, os números que queremos são aqueles que pertencem apenas ao conjunto de inteiros positivos.,
abaixo está a ligação algébrica entre o GCF e o LCM de dois inteiros positivos.
a fórmula GCF-LCM
aviso: realmente não existe tal coisa como a “fórmula GCF-LCM”. Acabei de inventar o nome para facilitar a referência. Pode chamar-lhe o que quiser, desde que sirva o seu propósito.,
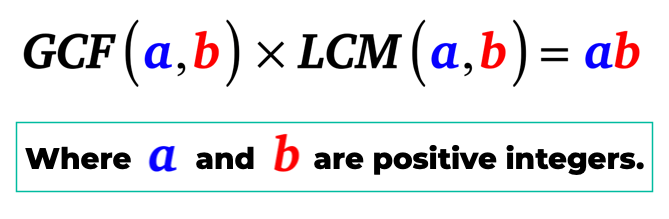
Simplesmente coloque, o maior fator comum de a e b, quando multiplicado para o mínimo múltiplo comum de a e b é igual ao produto de a e b. Isto é, a e b são números inteiros positivos.
Exemplo de Problemas
Exemplo 1: O GCF, de 12 e 16 é 4. O que é o LCM de 12 e 16?
pode determinar o LCM de 12 e 16 usando qualquer um dos dois métodos abaixo.,
- encontrando LCM usando o método da lista
- encontrando LCM usando o método de fatoração primária
No entanto, há uma maneira muito mais rápida. Você pode aproveitar a” fórmula GCF-LCM ” porque você conhece os dois inteiros e seu GCF. Basta ligar os valores na fórmula, em seguida, resolver para o LCM.
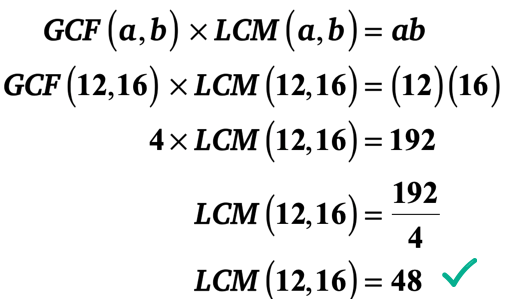
vou deixar que você verifique se o LCM de 12 e 16 é realmente 48.Exemplo 2: o LCM de 24 e 40 é de 120. O que é o GCF de 24 e 40?,
Este problema é o oposto exato do exemplo 1 porque você é dado o valor do LCM em vez de GCF.então estas são as informações que conhecemos. Vamos identificá-los para esclarecer.
▶︎ LCM(24,40) = 120
▶︎ a=24 e b=40, portanto, ab = \left( {24} \right)\left( {40} \right) = 960
📌 Nota: Isso realmente não importa o que os números são a e b. Isso não vai mudar o resultado da resposta final. No entanto, é uma boa prática padronizar a sua solução. Sugiro que deixe um ser o número inteiro menor, enquanto o b é o número inteiro maior.,
vamos substituir os valores conhecidos na fórmula então resolver para o GCF de 24 e 40.
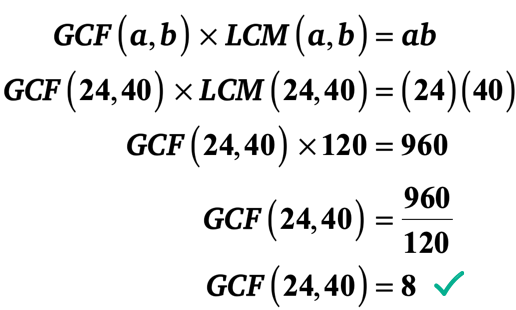
Exemplo 3: Encontrar o GCF de 20 e 25 por calcular o mínimo múltiplo comum de 20 e 25.
Este problema será um pouco diferente dos exemplos #1 e #2. Você terá que calcular primeiro o múltiplo menos comum (LCM) de 20 e 25. Depois disso, você pode resolver para o maior fator comum (GCF) de 20 e 25 usando a fórmula GCF-LCM.aqui vamos nós!, Para encontrar o LCM de 20 e 25, vamos escrever os primeiros múltiplos de 20 e 25. O primeiro múltiplo comum que aparece será o nosso LCM.
Múltiplos de 20: 20, 40, 60, 80, 100, 120
Múltiplos de 25: 25, 50, 75, 100, 125, 150
uma vez que o número de 100 mostra-se como a primeira múltiplo comum de 20 e 25, então podemos afirmar que o mínimo múltiplo comum de 20 e 25 é 100.
Agora temos todas as informações para usar a fórmula. Abaixo estão os valores que vamos substituir na fórmula para resolver o LCM de 20 e 25.,
◉ O produto de a e b → ab = \left( {20} \right)\left( {25} \right) = 500
◉ LCM de 20 e 25 → LCM\left( {20,25} \right) = 100
Aqui está o cálculo para resolver para o GCF de 20 e 25:
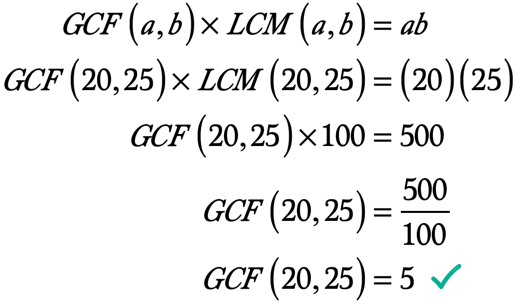
Exemplo 4: Encontrar o mínimo múltiplo comum de 63 e 84, calculando primeiro o GCF de 63 e 84.
Este problema é muito semelhante ao exemplo # 3. A única diferença é que você vai calcular primeiro o GCF em vez do LCM, como instruído pelo próprio problema.,vamos encontrar todos os fatores de 63 e 84. Você pode usar a técnica do “método arco-íris” para Fator os inteiros dados.
Notice that the largest or highest common factor between the two lists is 21.
Fatores de 63: 1, 3, 7, 9, 21, 63
Fatores de 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Portanto, o Maior Fator Comum de 63 e 84 é de 21 anos. Assim, GCF\esquerda ({63,84} \direita) = 21.,
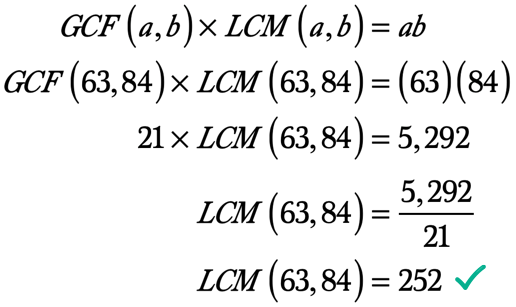
Exemplo 5: Encontrar o mínimo múltiplo comum de 72 e 90 usando o GCF-LCM Fórmula.
Como já sabemos, podemos encontrar o LCM de dois inteiros com o valor do seu GCF usando a fórmula GCF-LCM.,
Listagem de ambos os fatores de 72 e 90, tem-se:
Todos os fatores de 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Todos os fatores de 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Quando comparamos a lista de factores, vemos que 18 é o fator que é comum a ambos, mas tem o maior ou de maior valor. Significa que o FCF de 72 e 90 é de 18, ou seja, GCF\esquerda ({72,90} \direita) = 18.
estamos agora prontos para substituir os valores abaixo na fórmula.,
❖ ab = \left( {72} \right)\left( {90} \right) = 6,480
❖ GCF\left( {72,90} \right) = 18
Aqui está o cálculo para encontrar o LCM, dado que nós já sabemos o GCF de dois números inteiros e de seus produtos.