sequência
uma sequência é um conjunto de coisas (normalmente números) que estão em ordem.
sequências geométricas
numa sequência geométrica cada termo é encontrado multiplicando o termo anterior por uma constante.
em geral, escrevemos uma sequência geométrica como esta:
{a, ar, ar2, ar3, …, }
em que:
- a é o primeiro termo e
- r é o fator entre os termos (o chamado “comum ratio”)
Mas cuidado, r não deve ser 0:
- Quando r=0, obtemos a sequência {a,0,0,…} o que não é geométricas
A Regra
Nós também podemos calcular qualquer termo, utilizando a Regra:
xn = r(n-1)
(Nós usamos “n-1”, pois ar0 é para o 1º prazo)
Uma Seqüência Geométrica também pode ter menores valores:
Exemplo:
4, 2, 1, 0.5, 0.25, …,
esta sequência tem um factor de 0,5 (metade) entre cada número.
ua regra é xn = 4 × (0.5) n-1
Por Que sequência “geométrica”?,
Porque é como aumentar as dimensões em geometria:
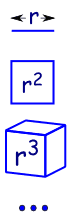 |
uma linha é 1-dimensional e tem um comprimento de r |
| em 2 dimensões, uma praça tem uma área de r2 | |
| em 3 dimensões de um cubo tem volume r3 | |
| etc (sim, nós podemos ter 4 ou mais dimensões em matemática)., |
sequências geométricas são por vezes chamadas de progressões geométricas (G. P.’s)
somando uma série geométrica
para somar estes:
a + ar + ar2 + … + ar(n-1)
(Cada termo é a arca, onde k começa em 0 e vai até n-1)
podemos usar este útil fórmula:

a é o primeiro termo
r é um “ratio” entre os termos
n é o número de termos
o Que é que engraçado Σ símbolo?, Ele é chamado de Notação Sigma
| (chamado Sigma) significa “soma” |
E abaixo e acima são mostrados os valores inicial e final:
Ele diz que “a Soma de n, onde n vai de 1 a 4. Resposta = 10
a fórmula é fácil de usar …, apenas “plug in” os valores de a, r e n
Usando a Fórmula
Vamos ver a fórmula na acção:
Exemplo: Grãos de Arroz em um Tabuleiro de Xadrez

Na página Dígitos Binários dar um exemplo de grãos de arroz em um tabuleiro de xadrez. Coloca-se a questão: quando colocamos arroz num tabuleiro de xadrez: 1 grão na primeira praça, 2 grãos na Segunda Praça, 4 grãos na terceira e assim por diante, 4 grãos na terceira e assim por diante…
… dobrando os grãos de arroz em cada quadrado …
…, quantos grãos de arroz no total?
Assim, temos:
- a = 1 (primeiro termo)
- r = 2 (dobra a cada hora)
- n = 64 (64 quadrados em um tabuleiro de xadrez)
Assim:

Torna-se:
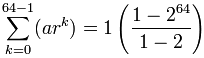
= 1-264-1 = 264 − 1
= 18,446,744,073,709,551,615
, Que era exatamente o resultado que conseguimos na Dígitos Binários página (graças a deus!)
e outro exemplo, desta vez com r inferior a 1:
por que a fórmula funciona?,
vamos ver por que a fórmula funciona, porque podemos usar um “truque” interessante que vale a pena saber.
nota que S E S·r são similares?agora subtrai-os!
Wow! Todos os Termos do meio cancelam.,
(Que é um truque)
subtraindo S·r de S, podemos obter um resultado simples:
S − S·r = a − arn
Vamos reorganizar-lo a encontrar S:
Qual é a nossa fórmula (ta-da!):

séries geométricas infinitas
então o que acontece quando n vai para o infinito?,
podemos usar a seguinte fórmula:
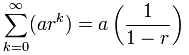
Mas atenção:
r deve estar entre (mas não incluindo) -1 e 1
e r não deve ser 0, pois a sequência {a,0,0,…} não é geométricas
Então, o nosso infnite série geométrica tem uma soma finita quando a proporção é de menos do que 1 (e maior do que -1)
Vamos trazer de volta o nosso exemplo anterior, e veja o que acontece:
|
não acredita em mim? Basta olhar para este quadrado: somando-se 12 + 14 + 18 + …acabamos com tudo!, |
 |
Recorrentes Decimal
Em outra página, pedimos “Não 0.999… equal 1?”, well, let us see if we can calculate it:



