
Neste artigo, você vai aprender sobre SVM ou Máquina de Vetor de Suporte, que é um dos mais populares AI algoritmos (ele é um dos top 10 AI algoritmos) e sobre o Kernel Trick, que lida com a não-linearidade e dimensões superiores., Vamos tocar temas como hiperplanos, multiplicadores de Lagrange, teremos exemplos visuais e exemplos de código (semelhante ao exemplo de código usado no capítulo KNN) para entender melhor este algoritmo muito importante.
SVM Explained
The Support Vector Machine is a supervised learning algorithm mostly used for classification but it can be used also for regression. A idéia principal é que com base nos dados rotulados (dados de treinamento) o algoritmo tenta encontrar o hiperplano ideal que pode ser usado para classificar novos pontos de dados. Em duas dimensões o hiperplano é uma linha simples.,
geralmente um algoritmo de aprendizagem tenta aprender as características mais comuns (o que diferencia uma classe de outra) de uma classe e a classificação é baseada nessas características representativas aprendidas (assim a classificação é baseada em diferenças entre classes). A SVM funciona ao contrário. Ele encontra os exemplos mais semelhantes entre classes. Esses serão os vetores de suporte.como exemplo, vamos considerar duas classes, maçãs e limões.,
outros algoritmos irão aprender as características mais evidentes e mais representativas de maçãs e limões, como as maçãs são verdes e arredondadas enquanto os limões são amarelos e têm forma elíptica.
em contraste, a SVM vai procurar maçãs que são muito semelhantes aos limões, por exemplo maçãs que são amarelas e têm forma elíptica. Este será um vector de suporte. O outro vector de suporte será um limão semelhante a uma maçã (verde e arredondado). Então outros algoritmos aprendem as diferenças enquanto a SVM aprende semelhanças.,
Se visualizamos o exemplo acima em 2D, vamos ter algo parecido com isto:

Como vamos da esquerda para a direita, todos os exemplos serão classificados como maçãs até chegar ao amarelo apple. A partir deste ponto, a confiança de que um novo exemplo é uma maçã cai enquanto a confiança da classe de limão aumenta., Quando a confiança da classe limão se torna maior do que a confiança da classe apple, os novos exemplos serão classificados como limões (em algum lugar entre a maçã amarela e o limão verde).com base nestes vetores de suporte, o algoritmo tenta encontrar o melhor hiperplano que separa as classes. No 2D, o hiperplano é uma linha, então ele teria esta aparência:

Ok, mas por que eu desenhe o azul fronteira como na imagem acima?, Eu também poderia desenhar limites como esta:

Como você pode ver, temos um número infinito de possibilidades para desenhar a decisão de limite. Então, como podemos encontrar o ideal?
encontrar o hiperplano ideal
intuitivamente a melhor linha é a linha que está longe tanto dos exemplos de maçã e limão (tem a maior margem)., Para ter a solução ideal, temos que maximizar a margem de ambas as maneiras (se temos várias classes, então temos que maximizá-la considerando cada uma das classes).

Então, se nós compare a foto acima com a foto abaixo, podemos facilmente observar que a primeira é a melhor hiperplano (linha) e a segunda é uma sub-solução ideal, porque a margem é muito menor.,

Porque queremos maximizar as margens de tomar em consideração todas as classes, em vez de usar uma margem para cada classe, utilizamos um “global” margem, que leva em consideração todas as classes., Esta margem seria parecido com a linha roxa na imagem a seguir:

Esta margem é ortogonal ao limite e equidistante para o suporte de vetores.então, onde temos Vectores? Cada um dos cálculos (calcular a distância e hiperplanos ótimos) são feitos em espaço vetorial, de modo que cada ponto de dados é considerado um vetor. A dimensão do espaço é definida pelo número de atributos dos exemplos., Para entender a matemática por trás, por favor leia esta breve descrição matemática de vetores, hiperplanos e otimizações: SVM sucintamente.todos os vetores de suporte são pontos de dados que definem a posição e a margem do hiperplano. Chamamos-lhes vetores de “suporte”, porque estes são os pontos de dados representativos das classes, se movermos um deles, a posição e/ou a margem irá mudar. Mover outros pontos de dados não terá efeito sobre a margem ou a posição do hiperplano.,
para fazer classificações, não precisamos de todos os pontos de dados de treinamento (como no caso da KNN), temos que salvar apenas os vetores de suporte. Na pior das hipóteses, todos os pontos serão vetores de suporte, mas isso é muito raro e se isso acontecer, então você deve verificar o seu modelo para erros ou bugs.
assim, basicamente, a aprendizagem é equivalente a encontrar o hiperplano com a melhor margem, então é um problema de otimização simples.,/h2>
Os passos básicos do SVM são:
- seleccione dois hyperplanes (em 2D) que separa os dados com pontos entre eles (linhas vermelhas)
- maximizar a sua distância (margem)
- linha média (aqui a linha de meio do caminho entre as duas linhas vermelhas) será a decisão de fronteira
Isso é muito bom e fácil, mas encontrar a melhor margem, o problema de otimização não é trivial (é fácil em 2D, quando temos apenas dois atributos, mas o que se tivermos N dimensões, com N um número bem grande)
Para resolver o problema de otimização, podemos usar os Multiplicadores de Lagrange., Para entender esta técnica, você pode ler os seguintes dois artigos: Multiplicador Duality Langrange e uma explicação simples de Por Que o Multiplicador Langrange Escreve.
até agora tínhamos dados separáveis linearmente, para que pudéssemos usar uma linha como limite de classe. Mas e se tivermos de lidar com conjuntos de dados não lineares?,
SVM Não-Linear Conjuntos de Dados
Um exemplo de não-linear de dados é:

Neste caso, podemos encontrar uma linha reta para separar as maçãs a partir de limão. Então, como podemos resolver este problema? Vamos usar o truque do Kernel!
a ideia básica é que quando um conjunto de dados é inseparável nas dimensões atuais, adicione outra dimensão, talvez dessa forma os dados serão separáveis., Basta pensar nisso, o exemplo acima está em 2D e é inseparável, mas talvez em 3D haja uma diferença entre as maçãs e os limões, talvez haja uma diferença de nível, então os limões estão no nível um e os limões estão no nível dois. Neste caso, podemos facilmente desenhar um hiperplano separador (em 3D um hiperplano é um plano) entre o Nível 1 e 2.
mapeamento para dimensões mais altas
para resolver este problema não devemos apenas adicionar cegamente outra dimensão, devemos transformar o espaço para gerar esta diferença de nível intencionalmente.,
mapeamento de 2D para 3D
vamos assumir que adicionamos outra dimensão chamada X3. Outra transformação importante é que na nova dimensão os pontos são organizados usando esta fórmula x12 + x22.
Se a gente traçar o plano definido por x2 + y2 fórmula, teremos algo como isto:

Agora temos que mapear as maçãs e limões (que são apenas simples pontos) para este novo espaço. Pensa bem, o que fizemos?, Acabamos de usar uma transformação na qual adicionamos níveis baseados na distância. Se você está na origem, então os pontos serão no nível mais baixo. À medida que nos afastamos da origem, isso significa que estamos subindo a colina (movendo-se do centro do plano em direção às margens) de modo que o nível dos pontos será maior., Agora, se considerarmos que a origem é o limão, a partir do centro, vamos ter algo parecido com isto:
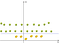
Agora podemos facilmente separar as duas classes. Estas transformações são chamadas de kernels. Kernels populares são: Kernel polinomial, Kernel Gaussiano, função de base Radial (RBF), kernel RBF Laplace, Kernel Sigmoid, Kernel RBF Anove, etc.,
Mapeamento de 1D a 2D
Outro exemplo mais fácil em 2D seria:

Depois de usar o kernel e depois de todas as transformações iremos obter:

Então, após a transformação, podemos facilmente delimitar as duas classes usando apenas uma única linha.,
em aplicações da vida real não teremos uma linha reta simples, mas teremos muitas curvas e dimensões altas. Em alguns casos, não teremos dois hiperplanos que separam os dados sem pontos entre eles, então precisamos de alguns compromissos, tolerância para os anómalos. Felizmente, o algoritmo SVM tem um chamado parâmetro de regularização para configurar o trade-off e tolerar anómalos.
Parâmetros de ajuste
como vimos na seção anterior, escolher o kernel certo é crucial, porque se a transformação é incorreta, então o modelo pode ter resultados muito pobres., Como regra geral, verifique sempre se você tem dados lineares e, nesse caso, use sempre SVM linear (kernel linear). Linear SVM é um modelo paramétrico, mas um kernel RBF SVM não é, de modo que a complexidade do último cresce com o tamanho do conjunto de treinamento. Não só é mais caro treinar um kernel RBF SVM, mas você também tem que manter a matriz do kernel ao redor, e a projeção para este espaço dimensional “infinito” superior onde os dados se tornam linearmente separáveis é mais caro também durante a previsão., Além disso, você tem mais hyperparameters para sintonizar, então a seleção de Modelos é mais caro também! E finalmente, é muito mais fácil exagerar um modelo complexo!
regularização
o parâmetro de Regularização (em python é chamado de C) diz à SVM optimization quanto você quer evitar perder a classificação de cada exemplo de treino.
Se o C é maior, a otimização escolherá um hiperplano de margem menor, de modo que a taxa de erro de classificação dos dados de treinamento será menor.,
Por outro lado, se o C é baixo, então a margem será grande, mesmo que haja exemplos de dados de treinamento classificados de falta. Isso é mostrado nos seguintes dois diagramas:

Como você pode ver na imagem, quando o C é baixa, a margem é maior (por isso, implicitamente não temos muitas curvas, a linha não segue estritamente os pontos de dados), mesmo se duas maçãs foram classificados como limões., Quando o C é alto, o limite está cheio de curvas e todos os dados de treinamento foram classificados corretamente. Não se esqueça, mesmo que todos os dados de treinamento foram corretamente classificados, isso não significa que o aumento do C vai sempre aumentar a precisão (por causa da sobrefitting).
Gama
o próximo parâmetro importante é o Gama. O parâmetro gama define até onde a influência de um único exemplo de treinamento alcança. Isto significa que o Gama elevado só considerará pontos próximos do hiperplano plausível e o Gama baixo considerará pontos a uma distância maior.,

Como você pode ver, diminuindo a Gama será o resultado do que encontrar a correta hiperplano irá considerar os pontos a distâncias maiores, de modo que mais e mais pontos vai ser usado (linha verde indica que os pontos foram considerados quando encontrar o melhor hiperplano).
margem
o último parâmetro é a margem. Já falamos de margem, maior resultado de margem melhor modelo, assim melhor classificação (ou previsão)., A margem deve ser sempre maximizada.
SVM Example using Python
In this example we will use the Social_Networks_Ads.ficheiro csv, o mesmo ficheiro que usamos no artigo anterior, veja o exemplo KNN usando Python.
neste exemplo vou escrever apenas as diferenças entre SVM e KNN, porque eu não quero me repetir em cada artigo! Se você quer toda a explicação sobre como podemos ler o conjunto de dados, como podemos analisar e dividir os nossos dados ou como podemos avaliar ou traçar os limites da decisão, então por favor leia o exemplo de código do capítulo anterior (KNN)!,
porque a biblioteca sklearn é uma biblioteca Python muito bem escrita e útil, nós não temos muito código para mudar. A única diferença é que temos que importar a classe VPC (VPC = SVM em sklearn) de sklearn.svm em vez da classe Knekhborsclassifier de sklearn.vizinho.
Depois de importar o VPC, podemos criar o nosso novo modelo usando o construtor predefinido. Este construtor tem muitos parâmetros, mas vou descrever apenas os mais importantes, na maioria das vezes você não vai usar outros parâmetros.,
os parâmetros mais importantes são:
- kernel: o tipo de kernel a ser usado. Os kernels mais comuns são rbf( este é o valor padrão), poli ou sigmoid, mas você também pode criar seu próprio kernel.,
- C: este é o parâmetro de regularização descrito no Ajuste de Parâmetros da secção
- gama: este também foi descrito no Ajuste de Parâmetros da secção
- grau: ele é usado somente se o escolhido kernel é poli e define o grau de polinom
- probabilidade: este é um parâmetro booleano e se é verdade, então o modelo de retorno para cada previsão, o vetor de probabilidades de pertencer a cada classe da variável de resposta. Então, basicamente, ele lhe dará as confidências para cada predição.,
- encolhimento: isto mostra se você quer ou não uma heurística encolhida usada na sua otimização da SVM, que é usada na otimização mínima Sequencial. Seu valor padrão é verdadeiro, e se você não tem uma boa razão, por favor, não mude este valor para falso, porque encolhimento irá melhorar muito o seu desempenho, por muito pouca perda em termos de precisão na maioria dos casos.
Agora vamos ver o resultado da execução deste código., A decisão de limite para o conjunto de treinamento parecido com este:

Como podemos ver e como aprendemos no Ajuste de Parâmetros da secção, porque o C tem um valor pequeno (0.1) a decisão de limite é suave.agora se aumentarmos o C de 0.,De 1 a 100, vamos ter mais curvas na decisão de fronteira:

o Que iria acontecer se usar C=0.1 mas agora vamos aumentar a Gama de 0,1 a 10? Vamos ver!

o Que aconteceu aqui? Porque temos um modelo tão mau?, Como viu na secção de Parâmetros de afinação, alta gama significa que, ao calcular o hiperplano plausível, consideramos apenas pontos que estão próximos. Agora, porque a densidade dos pontos verdes é alta apenas na região verde selecionada, nessa região os pontos estão próximos o suficiente para o hiperplano plausível, então esses hiperplanos foram escolhidos. Tenha cuidado com o parâmetro gama, porque isso pode ter uma má influência sobre os resultados de seu modelo, se você definir um valor muito alto (o que é um “valor muito alto” depende da densidade dos pontos de dados).,
para este exemplo, os melhores valores para C E gama são 1, 0 e 1, 0. Agora, se executar o nosso modelo no conjunto de teste, teremos o seguinte diagrama:

E a Matriz de Confusão parecido com este:

Como você pode ver, nós temos apenas 3 Falsos Positivos e 4 Negativos Falsos., A precisão deste modelo é de 93%, o que é um resultado realmente bom, obtivemos uma pontuação melhor do que usar o KNN (que tinha uma precisão de 80%).
nota: a precisão não é a única métrica usada em ML e também não é a melhor métrica para avaliar um modelo, por causa do Paradoxo da precisão. Nós usamos esta métrica para simplicidade, mas mais tarde, no capítulo métricas para avaliar algoritmos de IA vamos falar sobre o paradoxo da precisão e eu vou mostrar outras métricas muito populares usadas neste campo.,
conclusões
neste artigo vimos um algoritmo de aprendizagem supervisionado muito popular e poderoso, A Máquina de suporte vetorial. Aprendemos a idéia básica, o que é um hiperplano, o que são vetores de suporte e por que eles são tão importantes. Também vimos muitas representações visuais, o que nos ajudou a entender melhor todos os conceitos.
outro tópico importante que tocamos é o truque do Kernel, que nos ajudou a resolver problemas não-lineares.para ter um modelo melhor, vimos técnicas para afinar o algoritmo., No final do artigo tínhamos um exemplo de código em Python, que nos mostrou como podemos usar o algoritmo KNN.como pensamentos finais, gostaria de dar alguns prós & cons e alguns casos de uso popular.,
Vantagens
- SVN pode ser muito eficiente, pois utiliza apenas um subconjunto dos dados de treinamento, apenas os vetores de suporte
- Funciona muito bem em pequenos conjuntos de dados, em não-linear dos conjuntos de dados de alta dimensional espaços
- É muito eficaz em casos onde o número de dimensões é maior do que o número de amostras
- pode ter alta precisão, às vezes pode ter um desempenho ainda melhor do que as redes neurais
- Não é muito sensível para overfitting
Contras
- o tempo de Treinamento é alto quando temos grandes conjuntos de dados
- Quando o conjunto de dados tem mais de ruído (que eu.,e. destino classes são sobrepostos) SVM não executar bem
Popular Casos de Uso
- Classificação de Texto
- a Detecção de spam
- análise de Sentimento
- Aspecto baseado no reconhecimento
- Aspecto baseado no reconhecimento
- Manuscritas dígitos reconhecimento
