vad är termisk expansion?
termisk expansion är fenomenet där ett objekt eller en kropp expanderar som reaktion på att värmas upp. Termisk expansion är mest uppenbar i gaser och vätskor men kan fortfarande ha en väsentlig effekt på fasta ämnen.

Figure1: järnvägsspår böjda på grund av linjär termisk expansion
de termiska egenskaperna hos ett fast ämne är en mycket viktig aspekt i utformningen av fabriker och produkter., Om termisk expansion inte beaktas under konstruktion och design kan resultatet bli stora strukturella skador i en maskin eller byggnad. Otaliga åtgärder har vidtagits för att förhindra detta och många geniala tekniker utvecklas beroende av detta fenomen. Mängden som ett material expanderar kan förklaras med tanke på en koefficient som motsvarar materialets fraktionella tillväxt per grads temperaturförändring. Denna koefficient kallas värmeutvidgningskoefficienten och används för att förutsäga materialets tillväxt som svar på en känd temperaturförändring., Ju större denna koefficient är för ett material, desto mer kommer det att expandera per graders temperaturökning.
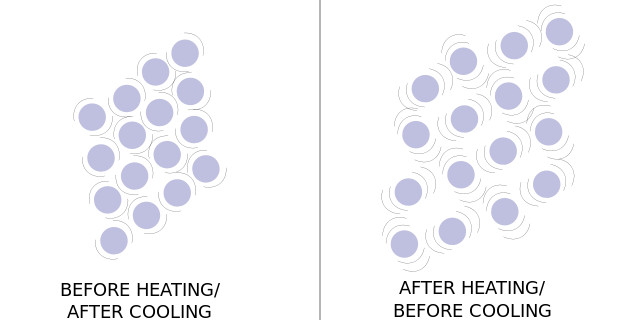
Figur 2: diagram över atomvibrationer före och efter uppvärmning.
när en kropp värms upp accepterar och lagrar den energi i sina atomer i form av kinetisk energi. Detta exponerar för en ökad temperatur orsakar en atoms naturliga vibrationer att växa starkare och mer uttalad., Denna ökning av vibrationer pressar mot de intermolekylära krafterna, vilket gör att atomer eller molekyler blir längre ifrån varandra och kroppen blir större. Mängden med vilken ett ämne expanderar som reaktion på en temperaturförändring representeras matematiskt av en värmeutvidgningskoefficient. Denna koefficient är unik för varje material och är baserad på deras andra fysikaliska egenskaper. Ju högre en värmeutvidgningskoefficient ett material har, desto mer kommer det att expandera som reaktion på att värmas upp., Kristaller tenderar att ha de lägsta termiska expansionskoefficienterna eftersom deras struktur är extremt likformig och strukturellt ljud. Diamond har den lägsta kända värmeutvidgningskoefficienten för alla naturligt förekommande material. De fasta ämnena med de högsta koefficienterna för termisk expansion är de som har svaga intermolekylära bindningar, typiskt polymerer, som också tenderar att ha låga smältpunkter. Anledningen till detta är att svagare bindningar övervinns med mindre vibrationell energi., Metaller tenderar att ha relativt låga koefficienter, men de har också mycket höga smältpunkter, och de är inte lika märkbara för ett materialfel som orsakas av expansionsspänningen. Detta gör metaller idealiska kandidater att använda vid mätning av termisk expansion.
mätningar av volymförändring orsakad av en fysikalisk eller kemisk process kallas dilatometri. Ett instrument som är utformat för att mäta volymförändringen av något ämne kallas en dilatometer., Det vanligaste exemplet på en dilatometer är en kvicksilvertermometer, som mäter volymen och förändringen i volymen av det fångade kvicksilvret som används för att bestämma temperaturen i den omgivande miljön. Dilatometrar kan också användas för att beräkna värmeutvidgningskoefficienten. För att bestämma koefficienten mäts materialets volym noggrant när temperaturen stiger från ett känt värde till ett annat. Det finns några exempel på dilatometrar som är utformade för att mäta volymen av fasta metallstycken för att bestämma termisk expansion., En design är kapacitansen dilatometrar. I denna design är en platta av en kondensator rörlig och provet placeras bakom det, så när det expanderar trycker det på den rörliga plattan närmare den andra plattan. Ett mer modernt och exakt exempel skulle vara laserdilatometern, som ständigt mäter provets dimensioner med lasrar. En av de mest mångsidiga mönster är den optiska dilatometer som är helt enkelt en digitalkamera med hjälp av en optisk grupp för att mäta variationer i provets storlek.,
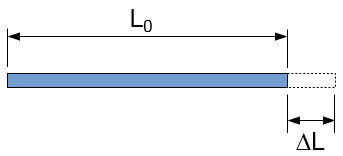
Figur 3: diagram som visar effekten av linjär termisk expansion.
gaser och vätskor expanderar alltid volymetriskt och expanderar inom ramen för sina behållare. I teorin expanderar fasta ämnen alltid volymetriskt också men eftersom de håller sin form gör det att de verkar expandera annorlunda. Till exempel, när en lång metallstav upphettas dess atomer färdas längre ifrån varandra i alla tre dimensioner. Under denna expansion kommer stavarna tvärsnittstillväxt knappast att märkas jämfört med dess tillväxt på längden., Eftersom stången är initialt mycket tunn finns det ett relativt litet antal atomer som skjuter mot varandra i tvärsnittsriktningen. I längdriktningen finns det dock ett större antal atomer uppradade, och när de alla trycker mot varandra bildar det en kedjereaktion som skjuter stångens totala längd för att vara mycket större än den var.
objekt med sådana dimensioner kan betraktas som enbart expanderande i en dimension. De tros ha en koefficient för linjär termisk expansion istället för en volymexpansionskoefficient., Denna koefficient fungerar på samma sätt som den tredimensionella expansionskoefficienten, förutom att den motsvarar den fraktionella ökningen i längd (istället för volym) per graderstemperatur. Detsamma gäller koefficienter för områdesexpansion i två dimensioner för plana plattor. Från denna observation kan det bestämmas att den mängd som en kropp expanderar som svar på en temperaturökning är linjärt beroende av kroppens ursprungliga storlek.
ett observationellt tillvägagångssätt kan antas för att hitta en användbar ekvation för att förutsäga den resulterande storleken på en kropp efter en temperaturförändring., Såsom förklaras ovan är den mängd som en linjär substans expanderar linjärt relaterad till den ursprungliga längden (L0). Observation visar att expansionen också är ungefär linjärt relaterad till temperaturförändringen (dT). Det är också uppenbart genom observation att alla material expanderar annorlunda. På grund av denna variation i expansionsmönster kan det bestämmas att andra fysiska aspekter påverkar termisk expansion. En koefficient används för att redovisa ett ämnes ytterligare fysikaliska egenskaper. Denna koefficient är känd som koefficienten för linjär termisk expansion, (α)., Ekvationen för den slutliga längden skulle därför vara
l = l0 + l0*α*dT
som kan ordnas för α
α = (L-L0) / (l0 * dT)
eller om det sägs att förändringen i längd, L-L0, är dL
α = 1 / l0 * dL/dt
samma logik kan användas för att bygga ekvationerna för volymexpansion. – herr talman! De är likartade, förutom att längdvariabeln skulle bytas ut mot volym och den linjära expansionskoefficienten skulle ändras till volymetrisk. För att säkerställa noggrannhet är den idealisk för att härleda volymexpansionsekvationen från den linjära ekvationen.,
v = L3 = 3
från analys med den linjära metoden är det uppenbart att värdet av α vanligtvis ligger i delarna per miljon intervall (x10-6). Eftersom värdet är så litet resulterar både de termer som höjer det till en kraft över en i ett så litet värde att de nästan inte kommer att påverka resultatet. Dessa villkor kan ignoreras genom att approximera något.
v = L03
= v0
eftersom α är en konstant okänd koefficient kan man säga att 3α är en ny konstant okänd koefficient som heter volymexpansionskoefficienten (β).,
v = V0 + V0*β*dT
β = 1/V0 * dv/dT
denna form av ekvationen kan nu användas för att hitta koefficienterna för termisk expansion av material efter mätning av dem med en dilatometer över en känd temperaturförändring. Dessa ekvationer visar att både de linjära och volymexpansionskoefficienterna har enheter av Kelvin-1, Celcius-1 eller Fahrenheit-1.
med en dilatometer och en termometer är det väldigt rakt fram att genomföra ett experiment på ett prov och följ sedan ekvationen för att beräkna de termiska expansionskoefficienterna., Aluminium är ett bekvämt material att studera med denna metod, eftersom det har en mycket hög expansionskoefficient för en metall. Rostfritt stål är kanske den vanligaste mätningen på grund av deras rikliga användning i många applikationer. Dessa stål har en koefficient som är ungefär Genomsnittlig för metaller, men de är inte extremt värdefulla som silver och guld. Brist på värmekunskap under teknik och design kan leda till att broar kollapsar eller förstöring av värdefull utrustning., Den termiska expansionen av material kan vara en viktig vägspärr för att bygga och designa, men många applikationsprocesser och tekniker har utformats med termisk expansion som en grundläggande funktionskomponent.

Figur 4: expansionsfog på en bro
