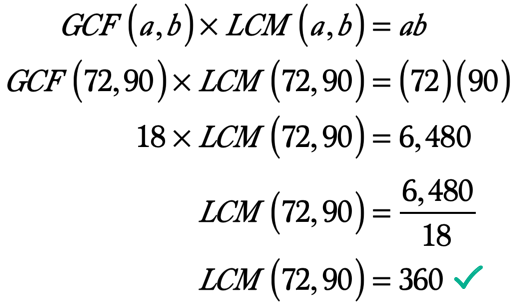da du studerede, hvordan du finder GCF og LCM af to positive tal, opdagede du et meget interessant forhold mellem de to mængder?

Jeg gjorde! Jeg opdagede det faktisk ved et uheld, da jeg var en ung studerende, og jeg troede, at jeg snuble over noget, der var “revolutionerende”. Jeg var så begejstret, at jeg delte det med min lærer., Men til min frustration så han på mig i øjet og sagde, at det allerede var en bevist matematisk erklæring. Jeg følte mig modløs et øjeblik, men jeg gik tilbage til mit skolearbejde og pressede på.

Hvis du ikke har fundet det endnu, er der et bemærkelsesværdigt algebraisk forhold eller forbindelse mellem den største fælles faktor (GCF) og det mindst almindelige multiplum (LCM) af to tal. I denne lektion er de tal, vi ønsker, dem, der kun tilhører sæt positive heltal.,
nedenfor er den algebraiske forbindelse mellem GCF og LCM af to positive heltal.
Den grønne klimafond-LCM Formel
ADVARSEL: Der er virkelig ikke sådan noget som “den grønne klimafond-LCM Formel”. Jeg har lige lavet navnet for nemheds skyld. Du kan kalde det noget, du ønsker, så længe det tjener sit formål.,
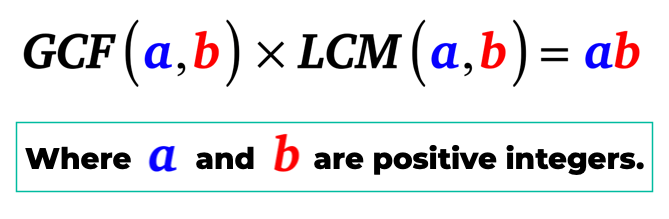
kort sagt, den største fælles faktor ganget til det mindst almindelige multiplum af A og B er lig med produktet af A og B. det vil sige, A og B er positive heltal.
Eksempelproblemer
eksempel 1: GCF på 12 og 16 er 4. Hvad er LCM på 12 og 16?
Du kan bestemme LCM på 12 og 16 ved hjælp af en af de to metoder nedenfor.,
- find LCM ved hjælp af Listemetoden
- find LCM ved hjælp af Primfaktoriseringsmetoden
Der er dog en meget hurtigere måde. Du kan drage fordel af “GCF-LCM-formlen”, fordi du kender de to heltal og dens GCF. Bare tilslut værdierne i formlen og løs derefter for LCM.
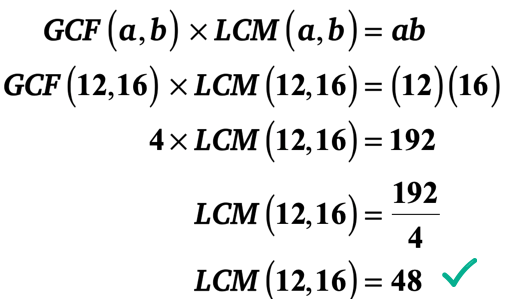
Jeg vil overlade det til dig at kontrollere, at LCM på 12 og 16 faktisk er 48.eksempel 2: LCM på 24 og 40 er 120. Hvad er GCF på 24 og 40?,
dette problem er det stik modsatte af Eksempel 1, fordi du får værdien af LCM i stedet for GCF.
så det er de oplysninger, vi kender. Lad os specificere dem for klarhed.
▶ ︎ LCM(24,40) = 120
therefore a=24 og B=40 derfor ab = \venstre( {24} \højre)\venstre( {40} \højre) = 960
note Bemærk: Det betyder ikke rigtig noget, hvilke tal der er A og B. det ændrer ikke resultatet af det endelige svar. Det er dog en god praksis at standardisere din løsning. Jeg foreslår, at du lader en være den mindre heltal, mens b være den større heltal.,
lad os erstatte de kendte værdier i formlen og derefter løse for GCF på 24 og 40.
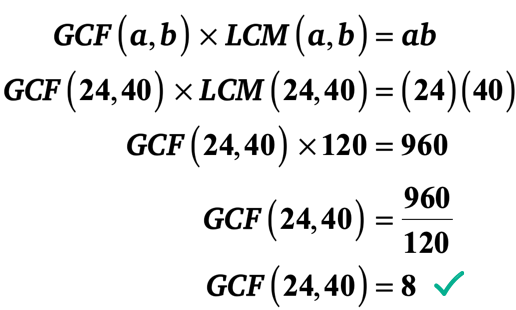
eksempel 3: Find GCF på 20 og 25 ved først at beregne LCM på 20 og 25.
dette problem vil være lidt anderledes end eksempler #1 og #2. Du skal først beregne det mindst almindelige multiplum (LCM) på 20 og 25. Derefter kan du løse for den største fælles faktor (GCF) på 20 og 25 ved at bruge GCF-LCM-formlen.
så her går vi!, For at finde LCM på 20 og 25 skriver vi de første par multipla på 20 og 25. Det allerførste fælles multiplum, der dukker op, vil være vores LCM.
multipla af 20: 20, 40, 60, 80, 100, 120
multipla af 25: 25, 50, 75, 100, 125, 150
da tallet 100 viser sig som det første fælles multiplum af 20 og 25, så kan vi hævde, at LCM af 20 og 25 er 100.
Vi har nu alle oplysninger til at bruge formlen. Nedenfor er de værdier, som vi vil erstatte i formlen til at løse for LCM på 20 og 25.,
product Produktet af A og b ab ab = \venstre( {20} \højre)\venstre( {25} \højre) = 500
◉ LCM på 20 og 25 and LCM\venstre( {20,25} \højre) = 100
Her er beregningen, der skal løses for GCF på 20 og 25:
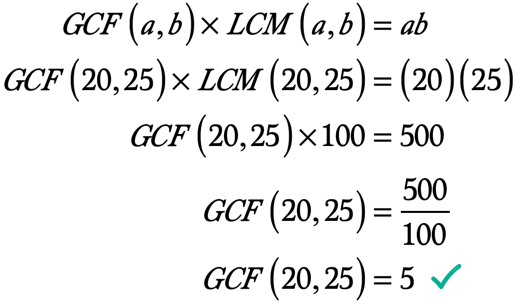
eksempel 4: Find LCM på 63 og 84 ved først at beregne GCF på 63 og 84.
dette problem ligner meget eksempel #3. Den eneste forskel er, at du først beregner GCF i stedet for LCM, som instrueret af selve problemet.,
lad os finde alle faktorer på 63 og 84. Du kan bruge” rainbo.method ” – teknikken til at faktor de givne heltal.
Bemærk, at den største eller højeste fælles faktor mellem de to lister er 21.
faktorer af 63: 1, 3, 7, 9, 21, 63
faktorer af 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
derfor er den største fælles faktor på 63 og 84 21. Således GCF \ venstre ({63,84} \højre) = 21.,
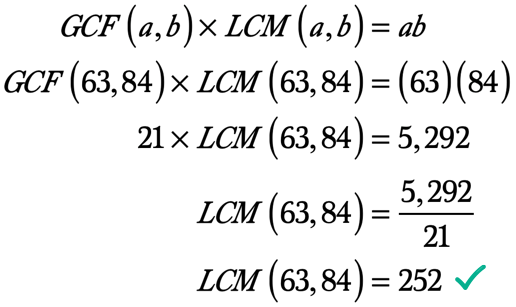
eksempel 5: Find LCM på 72 og 90 ved hjælp af GCF-LCM formlen.
som vi allerede ved, kan vi finde LCM af to heltal med værdien af dens GCF ved hjælp af GCF-LCM-formlen.,
viser både faktorerne 72 og 90, Vi har:
alle faktorer af 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
alle faktorer af 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Når vi sammenligner listerne over faktorer, ser vi, at 18 er den faktor, der er fælles for begge, men har den største eller største værdi. Det betyder, at GCF på 72 og 90 er 18, Det vil sige GCF\venstre( {72,90} \højre) = 18.
Vi er nu klar til at erstatte værdierne nedenfor i formlen.,
ab ab = \venstre( {72} \højre)\venstre( {90} \højre) = 6,480
❖ GCF\venstre( {72,90} \højre) = 18
Her er beregningen for at finde LCM, da vi allerede kender GCF for de to heltal og deres produkt.